
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

 |
Ce type de courbe algébrique (cubique) fut étudié par le marquis de l'Hospital et Huygens. Son nom latin (anguis = serpent) est dû à Newton quelques années plus tard (1701) qui la classa dans son Enumeratio linearum tertii ordinis (classification des courbes du 3ème ordre). Son équation cartésienne est de la forme :
![]() ,
a > 0 , b > 0
,
a > 0 , b > 0
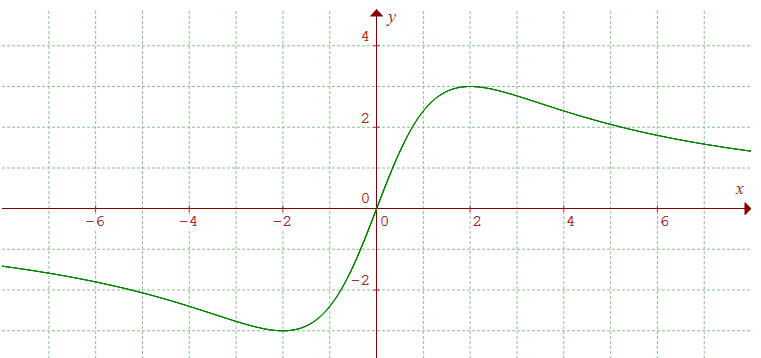
Ci-dessus : a = 2, b = 3

Sous une pierre le 8 avril 2006 - Seine & Marne -
France. Photographiée et rendue à la liberté !
| Génération géométrique : |
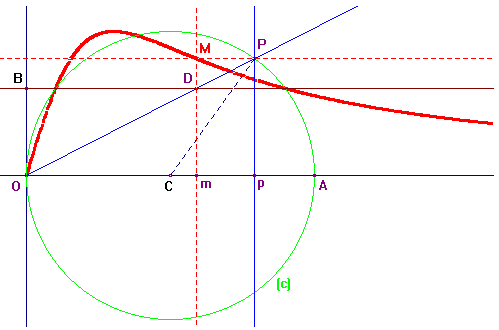
On peut générer géométriquement la restriction à R+ de la façon suivante : dans un repère orthonormé d'origine O, traçons le cercle (c) de centre C(a,0); soit B(0,b) avec 0 < b < a et P un point du cercle d'ordonnée positive. La parallèle à (Ox) passant par B coupe [OP) en D. Les parallèles à (Ox) passant par P et à (Oy) passant par D se coupent en M.
Lorsque P décrit le demi-cercle (OPA), M décrit la demi-anguinea.
En posant M(x,y), t = ^AOP, on a ^ACP = 2t et P(a + a.cos2t, asin2t); l'ordonnée y de M est celle de P. On obtient facilement x = b.cotan t (avec cotan = 1/tan cotangente) en remarquant que x/xP = Om/Op = Dm/Pp = b/y. On a ainsi une équation paramétrique de l'anguinea :
x = b.cotan t , y = asin2t
La serpentine est générée ci-dessous au moyen du logiciel de géométrie dynamique Cabri Géomètre, dans sa version CabriJava pour Internet :
L'égalité x = b.cotan t conduit à : xsin2t = b2cos2t. Dans le 1er membre, on remplace sin2t par 1 - cos2t, on obtient alors :
cos2t x (x2 + b2) = x2
La relation x/xP = b/y peut s'écrire : xy = bxP, soit xy = 2abcos2t. On peut ainsi éliminer cos2t, ce qui fournit :

Si votre navigateur accepte les applets
Java
(»
extension CheerpJ![]() ) :
) :
Déplacer P (pas "trop"
vite); pour effacer le lieu
double-cliquer dans la figure