ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
De l'HOSPITAL Guillaume, français, 1661-1704 |
Guillaume François Antoine de l'Hospital,
comte d'Autremont, marquis de Saint-Mesme apprit les mathématiques auprès de
Johann
Bernoulli (Jean), le frère cadet de Jakob
(Jacques).
On
ne le confondra pas avec Michel de l'Hospital (1505-1573, à droite),
conseiller au parlement de Paris, surintendant des finances puis nommé
chancelier de France par Catherine de Médicis, épouse du roi de
France Henri II. Ce grand serviteur du royaume joua un important rôle
de pacificateur entre catholiques et protestants mais mourut peu après
la Saint-Barthélemy qu'il ne put empêcher car disgracié
en 1568.
Membre de l'Académie Royale des Sciences (1693), Guillaume de l'Hospital, s'inspirant des travaux de son "maître" et en accord avec lui, édita en 1696 un traité complet de calcul différentiel : Analyse des infiniment petits pour l'intelligence des lignes courbes (le terme intelligence est utilisé ici au sens de compréhension) qui marquera, avec les travaux de Leibniz et Newton, l'avènement des méthodes différentielles et du calcul intégral.
➔ Dans cet ouvrage, l'Hospital sera le premier à utiliser le terme français d'intégrale d'une fonction f (issu du latin médiéval integralis utilisé par Jakob et Johann Bernoulli) pour désigner la fonction F dont la différentielle (il parlait à l'époque de différence) est f(x)dx. Il semble être aussi à l'origine du terme analyse pour désigner cette nouvelle branche mathématique du calcul différentiel et intégral. Le terme fonction est dû à Leibniz.
l'Hospital résolut le problème de la courbe brachistochrone en même temps que Leibniz et Newton, répondant au défi de Johann.
A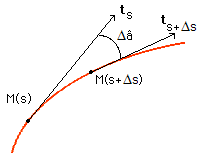
u
sujet des lignes courbes, il écrit
qu'elles doivent être considérées l'assemblage
d'une infinité de lignes droites, chacune infiniment petite ou, ce qui est la
même chose, comme un polygone d'un nombre infini de côtés,
chacun infiniment
petit, dont les angles qu'ils font entre eux déterminent la courbure de la ligne.
C'est encore l'acception d'aujourd'hui qui étudie la courbure en un point M en étudiant l'angle formé par les tangentes en M et M + ΔM infiniment proche de M.
Courbure d'un courbe plane ou gauche : »
On lui doit un traité conséquent sur les sections coniques (Traité analytique de sections coniques et de leur usage pour la résolutions des équations), qu'il traite tant par des méthodes géométriques et analytiques (équations de la forme ax2 + bx2 + cxy + dx + ey + f = 0). Finalisé en 1699, il ne fut publié qu'après sa mort à la demande de Fontenelle alors secrétaire de l'Académie Royale. Le traité est disponible sur Google Livres à cette adresse.
Wallis et l'étude analytique des sections coniques : »
| Règle de l'Hospital pour le calcul d'une limite se présentant sous la forme indéterminée 0/0 : |
f et g sont des fonctions numériques continues sur un voisinage V d'un réel xo, dérivables sur V (sauf éventuellement en xo) et vérifiant f(xo) = g(xo) = 0. On suppose en outre que g' est non nulle sur V (sauf peut-être en xo). Dans ces conditions, si f '/g' admet une limite en xo (finie ou non), alors f/g admet la même limite en xo.
Par exemple :
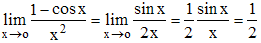
➔ Si la forme f '/g' est encore indéterminée (forme 0/0), qu'à cela ne tienne : passez à f ''/g'', f '''/g'''... (si ces dérivées vérifient les conditions d'usage de la règle initiale). Avec un peu de chance, vous finirez par vous en sortir !
Par exemple, soit à calculer L = lim x → o (x - sin x)/x3. On a successivement :
L = lim x → o (1 - cos x)/3x2 = lim x →o sin x/6x = lim x → o cos x /6 = 1/6
Notons que les continuités en xo de f ' et de g' ne sont pas nécessaires (la démonstration de la règle est conséquence du théorème des accroissements finis généralisés) et que la réciproque de cette règle est fausse comme le prouve l'exemple suivant : au voisinage de zéro, prenez f(x) = x2cos(1/x) prolongée en 0 par 0 et g(x) = sin x.
Étude de x2cos(1/x) : »
Ce résultat pratique s'applique dans des conditions semblables au cas de fonctions d'une variable complexe en remplaçant dérivables par holomorphes (ou analytiques) au voisinage d'un complexe zo.
Jean Bernoulli 1er