ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Quadrature selon l'Encyclopédie de Diderot et d'Alembert

 ➔   Texte original. Seuls sont modifiés la mise en page, quelques tournures et aspects orthographiques ou grammaticaux Les mots ou les commentaires en vert sont ajoutés pour une meilleure compréhension.

 QUADRATURE, s. f. terme de Géométrie ; manière de quarrer ou de réduire une figure en un quarré (carré), ou de trouver un quarré égal à une figure proposée.

Ainsi la quadrature d'un cercle, d'une parabole, d'une ellipse, d'un triangle, ou autre figure semblable, consiste à faire un quarré égal en surface à l'une ou à l'autre de ces figures.

La quadrature des figures rectilignes est du ressort de la géométrie élémentaire ; il ne s'agit que de trouver leurs aires ou superficie et de la transformer en un parallélogramme rectangle.

Il est facile ensuite d'avoir un quarré égal à ce rectangle, puisqu'il ne faut pour cela que trouver une moyenne proportionnelle entre les deux côtés du rectangle.

» dans ChronoMath, voyez : quadrature

La quadrature des courbes, c'est-à-dire la manière de mesurer leur surface, ou de trouver un espace rectiligne égal à un espace curviligne, est une matière d'une spéculation plus profonde, et qui fait partie de la Géométrie sublime. Archimède paraît être le premier qui ait donné la quadrature d'un espace curviligne, en trouvant la quadrature de la parabole.

Quoique la quadrature des figures, surtout celle du cercle, ait été l'objet de l'application des plus fameux mathématiciens de l'antiquité, on peut dire qu'on n'a rien fait de considérable sur cette matière, que vers le milieu du dernier siècle ; savoir en 1657, que MM. Neil & Brounker, & après eux M. Christophle Wren, ont trouvé les moyens de démontrer géométriquement l'égalité de quelques espaces curvilignes courbes, avec des espaces rectilignes.

Quelques tems (temps) après, plusieurs géomètres, tant anglais que des autres nations, firent les mêmes tentatives sur d'autres courbes, & réduisirent le problème au calcul analytique. Mercator en publia pour la première fois l'essai en 1688, dans une démonstration de la quadrature de l'hyperbole de milord Brounker, dans laquelle il se servit de la méthode de Wallis pour réduire une fraction en une suite infinie par le moyen de la division.

Il paraît cependant, pour le dire en passant, que M. Newton avait déjà découvert le moyen de trouver la quadrature des courbes par sa méthode des fluxions, avant l'année 1668. Voyez FLUXION.

» dans ChronoMath, voyez : fluxion , fluxion selon d'Alembert

Messieurs Christophe Wren & Huygens se disputent la gloire d'avoir découvert la quadrature d'une portion de la cycloïde. M. Leibnitz découvrit ensuite celle d'une autre portion ; & en 1699. M. Bernoulli découvrit celle d'une infinité de segments & de secteurs de cycloïde. Voyez les mém. de l'acad. de 1699.

QUADRATURE DU CERCLE, est la manière de trouver un quarré égal à un cercle donné. Ce problème a occupé inutilement les mathématiciens de tous les siècles. Voyez CERCLE.

Il se réduit à déterminer le rapport du diamètre à la circonférence, ce qu'on n'a pu faire encore jusqu'ici avec précision.

Si ce rapport était connu, on aurait aisément la quadrature du cercle, puisqu'il est démontré que sa surface est égale à celle d'un triangle rectangle qui a pour hauteur le rayon du cercle, & pour base une ligne égale à sa circonférence. Il n'est donc besoin pour quarrer le cercle que de le rectifier. Voyez CIRCONFERENCE & RECTIFICATION.

» dans ChronoMath, voyez : Le cercle ,  rectification

Le problème de la quadrature du cercle consiste proprement dans l'alternative de trouver cette quadrature ou de la démontrer impossible. La plupart des géomètres n'entendent par quadrature du cercle que la première partie de cette alternative ; cependant la seconde résoudrait parfaitement le problème.

M. Newton a déjà démontré dans le premier livre de ses principes mathématiques, sect. VI. tom. XXVIII. que la quadrature indéfinie du cercle, & en général de toute courbe ovale, était impossible, c'est-à-dire qu'on ne pouvait trouver une méthode pour quarrer à volonté une portion quelconque de l'aire du cercle ; mais il n'est pas encore prouvé qu'on ne puisse avoir la quadrature absolue du cercle entier. Si on avait le rapport du diamètre à la circonférence, on aurait, comme on l'a déjà dit, la quadrature du cercle, d'où il suit que pour quarrer le cercle il suffit de le rectifier, ou plutôt que l'un ne peut se faire sans l'autre.

Il n'y a point de courbe qui réellement & en elle-même ne soit égale à quelque ligne droite, car il n'y en a point que l'on ne puisse concevoir exactement enveloppée d'un fil, & puis développée ; mais il faut pour les géomètres que ce qu'ils connaissent de la nature de la courbe puisse leur servir à trouver cette ligne droite, ou ce qui revient au même, il faut que cette ligne soit renfermée dans des rapports connus, de manière à pouvoir elle-même être exactement connue. Or quoiqu'elle y soit toujours renfermée, elle ne l'est pas toujours de la manière dont nous aurions besoin ; au-delà d'un certain point, qui n'est pas même fort éloigné, nos lumières nous abandonnent & aboutissent à des ténèbres.

Ceux qui désireront un plus grand détail sur la quadrature du cercle, peuvent avoir recours à l'ouvrage que M. Montucla a publié en 1754. sur ce sujet, sous le titre d'histoire des recherches sur la quadrature du cercle. Ils y trouveront un récit fidèle, savant & raisonné des travaux des plus grands géomètres sur cette matière, & ils y apprendront à se prémunir contre les promesses, les jactances & les inepties des quadrateurs. Une de leurs principales prétentions est de croire que le problème de la quadrature du cercle est fort important pour les longitudes ; en quoi ils se trompent grossièrement, ces deux problèmes n'ayant aucun rapport.

 i  Jean Etienne Montucla, français  (1725-1799) : avocat à Toulouse, il "monte" à Paris où il reprend des études scientifiques. Astronome à la cour du roi Louis XV, il publia (1754)  une Histoire des recherches sur la quadrature du cercle (1754) puis (1758) une histoire des mathématiques (2 tomes) qui eut une forte audience auprès de la communauté scientifique; elle sera complétée (1802) par l'astronome et académicien Joseph J. Lalande. A noter : Montucla fut aussi secrétaire (on dirait aujourd'hui directeur de cabinet) de Turgot, philosophe, économiste et ministre des finances sous Louis XV, qui signa dans l'encyclopédie de Diderot et d'Alembert, différents articles dont celui sur l'étymologie.

Plusieurs géomètres ont approché fort près de ce rapport. Archimède paraît avoir été un des premiers qui ont tenté de le découvrir, & a trouvé par le moyen des polygones réguliers de 96 côtés inscrits & circonscrits au cercle, que ce rapport est comme 7 à 22. Voyez POLYGONE.

» dans ChronoMath, voyez : polygones , polygones réguliers

Quelques-uns des modernes ont approché beaucoup plus près, surtout Ludolphe de Ceulen (inconnu au bataillon...) qui a trouvé après des calculs infinis, qu'en supposant que ce diamètre soit 1, la circonférence est plus petite que 3,14159265358979323846264338387950 ; mais plus grande que ce même nombre en mettant l'unité pour dernier chiffre.

» le 8 marqué en rouge est inexact, c'est un 2 : sans doute une erreur au niveau de l'imprimeur qui aura mal lu car les autres décimales sont justes ! C'est un résultat fabuleux pour l'époque.

Les géomètres ont encore eu recours à d'autres moyens, surtout à des espèces de courbes particulières qu'on appelle quadratrices ; mais comme ces courbes sont mécaniques ou transcendantes, & non point géométriques, elle ne satisfait point exactement à la solution du problème. Voyez TRANSCENDANT, MECHANISME & QUADRATRICE.

» dans ChronoMath, voyez : Dinostrate , quadrature du cercle ,  transcendants (nombres)

On a donc employé à l'analyse, & tenté de résoudre ce problème par plusieurs méthodes différentes, & principalement en employant certaines séries qui donnent la quadrature approchée du cercle par une progression de termes. Voyez SERIE ou SUITE.

» dans ChronoMath, voyez : suites , séries

En cherchant par exemple une ligne droite (un segment) égale à la circonférence d'un cercle, on trouve en supposant pour le diamètre que la circonférence doit être

qui forment une suite infinie de fractions dont le numérateur est toujours 4, & dont les dénominateurs sont dans la suite naturelle des nombres inégaux ; & tous ces termes sont alternativement trop grands & trop petits.

» dans ChronoMath, voyez : calcul de π selon Gregory

Si l'on pouvait trouver la somme de cette suite, on aurait la quadrature du cercle ; mais on ne l'a point encore trouvée, & il y a même apparence qu'on ne la découvrira de longtemps. On n'a point cependant démontré que la chose soit impossible, ni par conséquent que la quadrature du cercle le soit aussi.

» voir, plus récemment : Wantzel

D'ailleurs comme on peut exprimer la même grandeur par différentes séries, il peut se faire aussi que l'on puisse exprimer la circonférence d'un cercle par quelque autre série dont on puisse trouver la somme. Nous avons deux suites infinies qui expriment la raison de la circonférence au diamètre, quoique d'une manière indéfinie. La première a été découverte par M. Newton, qui a trouvé, en supposant pour le rayon, que le quart de la circonférence est

La seconde est de M. Leibnitz, qui trouve de même que le rayon étant l'arc de 45 degrés, est la moitié de

Voici la manière de trouver chacune de ces séries par le calcul intégral ; on la doit à M. Newton.

Quadrature du cercle par M. Newton : soit le rayon du cercle AC = 1 (Planch. d'anal. fig. 24) CP = x, y = & = 1 - x²/2 - x⁴/8 - x⁶/16 - 5x⁸/128 - 7x¹⁰/256, &c. à l'infini.   

» série du binôme ;  noter ci-contre quelques erreurs de l'imprimeur...

Donc PpmM ou ydx = dx - x²dx/2  - x⁴dx/8 - x⁶dx/16 - 5x⁸dx/128 - 7x¹⁰dx/256, &c. à l'infini. Et ∫ydx = x - x³/6 - x⁵/40 - x⁷/112 - 5x⁹/1152 - 7x¹¹/2816 &c. à l'infini.

Lorsque x devient égal au rayon CA, l'espace DCPM se change en un quart de cercle. Substituant donc 1 à x, le quart de cercle sera 1 - 1/6 - 1/40 - 1/112 - 5/1152 - 7/2816, &c. à l'infini. Cette même série peut servir à mesurer la surface entière du cercle, en supposant son diamètre = 1.

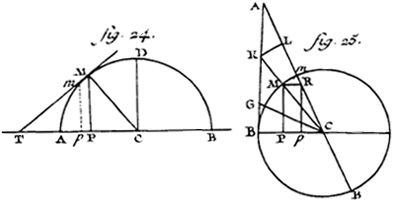
»  plutôt diamètre = 2 ?!? le développement donné 1 - 1/6 - 1/40 - 1/112 - 5/1152- 7/2816 &c. à l'infini, fournit π/4 "très lentement".   » Jones.

Quadrature du cercle par M. Leibnitz : soit la tangente KB = x (Pl. d'analyse fig. 25.), BC = 1 ; la sécante AC infiniment proche de CK ; décrivez avec le rayon CK le petit arc KL : vous aurez AK = dx, KC = √(1 + x²) car KC2 = 1 + x² dans KBC rectangle en B. Maintenant puisque les angles B & L sont droits, & l'angle BKC = KAC, à cause de la petitesse infinie de l'angle KCL, nous aurons :

KC : BC : : KA : KL  (correction erreur dans le texte) , c'est-à-dire √(1 + x²) : 1 : : d x : dx/√(1 + x²)
De plus, CK : KL : : CM : mM ; c'est-à-dire √(1 + x²) : dx/√(1 + x²) : : 1 : dx/(1 + x²)

» Rappelons ici qu'autrefois les proportions a/b = c/d étaient notées a:b :: c:d pour signifier « a est à b ce que c est à d »; par exemple 2 est à 8 ce que 25 est à 100, c'est à dire le quart... les « : » ont le sens usuel de la division et les « :: » peuvent se lire «est équivalent à ».

Donc le secteur CMm = ½dx : (1 + x²) = ½(d x - x²dx + x⁴dx - x⁶dx + x⁸dx - x¹⁰dx, &c.) & l'on trouve, par le calcul intégral, le secteur BCM (dont la tangente KB est x) x/2 + x³/6 + x⁵/10 - x⁷/14 + x⁹/18 - x¹¹/22 &c. & ainsi à l'infini. C'est pourquoi si BM est la huitième partie du cercle ou un arc de 45d. (45 degrés, alors KB = 1) le secteur sera 1/2 - 1/6 + 1/10 - 1/14 &c. à l'infini.
Donc le double de cette série 1 - 1/3 + 1/5 - 1/7 + 1/9 - 1/11 &c. à l'infini, est le quart de cercle (en terme d'aire! et comme KB = 1, cette série converge vers π × 12/4 = π/4  → calcul de π selon Gregory).

D'Alembert traite ensuite de la quadrature des lunes d'Hippocrate de Chio « le premier qui ait quarré une portion du cercle à qui sa figure a fait donner le nom de lunule », de la quadrature de l'ellipse, de la parabole, de l'hyperbole et de l'arche de cycloïde (en prouvant qu'elle est le triple de son cercle générateur) et de quelques autres courbes.

Intégrale selon d'Alembert :  »