
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
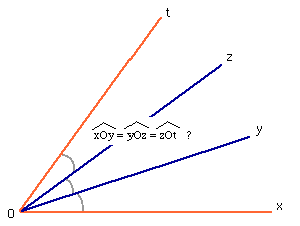
La quadratrice de Dinostrate, en fait la trisectrice d'Hippias, permet de trisecter un angle (et plus généralement de construire toute section d'un angle donné). Rappelons le problème dont Wantzel a montré l'insolubilité en 1837 :
Étant
donné un angle ^xOt, peut-on, à l'aide de la
règle et du compas construire [Oy) et [Oz)
tels
que ^xOy = ^yOz = ^zOt ?
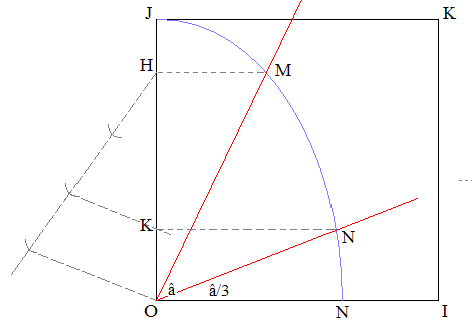
Supposons la quadratrice Q tracée dans un repère (O,I,J) et désignons par y l'ordonnée de M sur Q.
à des déplacements égaux de [HM] depuis la position ]JK[ correspondent des variations angulaires égales car, selon l'étude de la quadratrice, lerapport y/â est constant sur Q.
Par conséquent, si on se donne un angle ^IOM de mesure â avec M, situé sur la quadratrice, se projetant en H sur [OJ], on obtiendra ^ION de mesure â/3 en construisant K tel que OK = OH/3 au moyen de la propriété de Thalès, afin de fournir le point N cherché sur Q.
Trisection selon Thomas Céva : »