ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Quadrangle (ou quadrilatère) harmonique

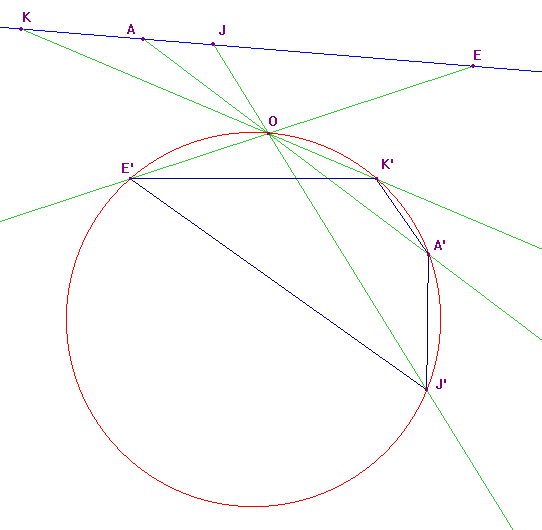
Considérons une division harmonique [K,J,A,E] sur une droite (d) et un point O non situé sur (d). Appelons K', J', A', et E' les images des points K, J, A, E dans une inversion de pôle O; on obtient un quadrilatère ayant la propriété remarquable d'être inscriptible (ses sommets sont sur un même cercle) : on parle de quadrangle (ou  quadrilatère) harmonique.

De plus :

• le produit de deux quelconques de ses côtés est constant : c'est la moitié du produit des diagonales.

Sur la figure ci-dessous, la division [K,J,A,E] est harmonique.
Les images par inversion de pôle O ont été construites en utilisant la propriété étudiée en exercice : si K' est donné, alors les points K,A,K et A' sont cocycliques.

La figure ci-dessous est générée au moyen du logiciel de géométrie dynamique Cabri Géomètre, dans sa version CabriJava pour Internet :

Si votre navigateur accepte les applets Java (» extension CheerpJ) :
Vous pouvez déplacer les points A, E et K'  ainsi que la droite (AE).

»  Quadrilatère complet | Quadrangle complet

 ➔    Pour en savoir plus :

• GEOMETRIE, classe de mathématiques élémentaires par V. Lespinard et R. Pernet, Librairie A. Desvigne - Lyon, 1962.
• Géométrie classique et mathématiques modernes par Brigitte Sénéchal - Formation des enseignants et formation continue - Ed. Hermann - Paris 1979