
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
|
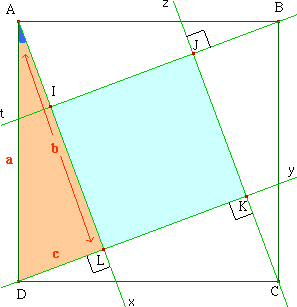
1. Prouver que IJKL est un carré.
2. Les quatre triangles ADL, DKC, CJB et AIB sont rectangles et isométriques (mêmes mesures). On pose AD = a, DL = c et AL = b. Montrer que :
➔ On pourra s'inspirer de la preuve analogue donnée à la page Pythagore : »