ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Théorème de Pythagore  selon Bhaskara  #1         » variante #2

La preuve doit être simple, car selon Bhaskara, Regardez !  est le seul argument de sa démonstration...

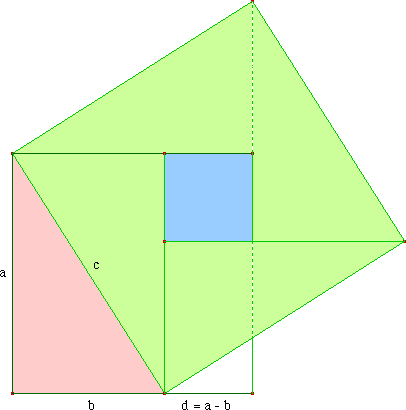
C'est effectivement pas très compliqué, mais ingénieux :

• En bleu : un "petit" carré de côté a - b.
• on reporte b (deux fois) à l'extérieur du "grand" carré de côté a. Ok ?
• on obtient le grand carré "diagonal" de côté c qui est l'hypoténuse du triangle rectangle
  de côtés a et b
• on a c² = (a - b)² + 4 × ab/2, soit c² = a² + b² car depuis Al Khwarizmi, voire depuis Euclide, on sait que : (a - b)² = a² - 2ab + b², identité remarquable chère au yeux des élèves de 3ème...