ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Polyèdres réguliers étoilés (croisés) de Kepler & Poinsot           »  Polygones étoilés , Polyèdres réguliers convexes , Polyèdres archimédiens , Pacioli , Penrose , Johnson

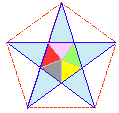Considérons un polyèdre dont les faces sont des pentagones réguliers croisés (pentagones étoilés), autrement dit des pentagrammes comme ci-contre en bleu ciel, le centre a été "décoré" pour coller à l'étude qui suit :

Vous devez maintenant plonger dans la 3ème dimension en contemplant le très beau polyèdre ci-dessous, dit petit dodécaèdre étoilé. Le pentagramme "de base" est en en bleu ciel vu du "dessus". On peut accoler 5 autres pentagrammes identiques :

•  rouge : "nord-ouest"      •  rose : "nord-est"      •  vert : "est"
•  jaune : "dessous"           •  gris : sud-ouest

de sorte qu'ils forment 5 pyramides régulières dont la base est un pentagone régulier :

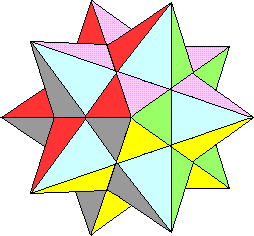
La somme des angles d'un pentagone est 180 × 3 = 540° puisqu'il se décompose en 3 triangles. Les angles de chaque branche mesurent 108°/3 = 36° (3 angles inscrits interceptant des arcs égaux étant égaux). Rappelons que cos(36°) = Φ/2, moitié du nombre d'or.

On démontre que le solide obtenu se referme de toutes parts et, ce faisant, on obtient 6 autres pentagrammes (faces cachées) : c'est un des deux dodécaèdres (12 faces) étoilés réguliers découverts par Kepler : les faces sont isométriques et les angles d'arêtes de leurs angles polyèdres mesurent tous 36°. Le second s'obtient plus subtilement : les centres de chaque face sont le centre de la sphère circonscrite au polyèdre.

Poinsot exhiba deux autres polyèdres réguliers non convexes : un icosaèdre (20 faces) et un dodécaèdre, dit grand dodécaèdre (ci-dessous). Cauchy prouva qu'il n'en existait pas d'autres.

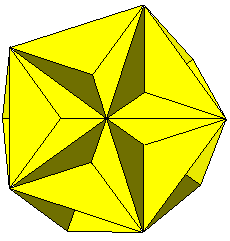
On trouvera les quatre polyèdres, superbes et animés de surcroît, sur le site Hubert Martineau (réf.1 ci-dessous).

 ➔   Pour en savoir plus :

1. Le site de Hubert Martineau : http://math.lemur.pagesperso-orange.fr/3d/kepler.htm

2. Le livre de Yvonne et René Sortais : Géométrie de l'espace et du plan Ed. Hermann , 1988 -Coll. Formation des Enseignants/Formation continue.

3. Le site Mathcurve de Robert Ferréol : http://www.mathcurve.com/polyedres/keplerpoinsot/keplerpoinsot.shtml

4. L'article de Sylvain Crovisier dans Quadrature n° 66 (oct-déc. 2007) : http://www.annales.org/archives/x/q06013.pdf

5. Une chronologie des polyèdres sur CultureMath : http://www.dma.ens.fr/culturemath/video/Dupas-polyedres/ Dupas-chrono.htm

6. Une foule de polyèdres animés sur Pedagoguery Software Inc. (Canada). Vous pourrez y télécharger un
   logiciel générateur : http://www.peda.com/poly/ et http://www.peda.com/download (logiciel générateur).