
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
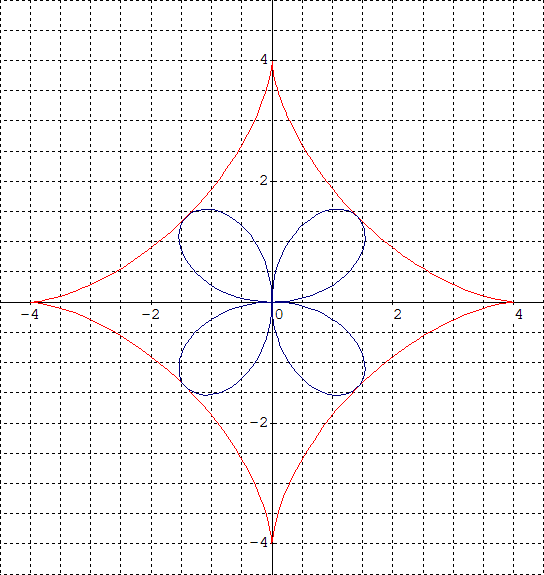
» Quadrifolium (étude polaire directe) | Développée de l'astroïde |
 |
L'astroïde a pour équation paramétrique :
Selon la théorie, l'équation de la podaire par rapport à O sera :
ce qui conduit sans difficultés aux relations x'2 + y'2 = 18 - 18cos 4t et xy' - yx' = 6 - 6cos 4t
D'où l'équation de la podaire et la courbe représentée ci-dessous en bleu par Graphmatica :
X = cos t - cos 3t , Y = sin t + sin 3t , t variant sur [0,2π] ou [-π,+π]
Mais le quadrifolium, direz-vous, est plutôt connu par son équation polaire de la forme :
x = a.sin2 t.cos t , y = a.cos2 t.sin t
Or :
cos3t = cos(2t + t) = cos 2t.cos t - sin 2t.sin t
sin 3t = sin 2t.cos t + sin t.cos 2t
1 - cos 2t = 2sin2t
1 + cos 2t = 2cos2t
sin 2t = 2sin t.cos t
Partant de notre podaire d'équation X = cos t - cos 3t , Y = sin t + sin 3t, nous avons :
X = cos t - cos 3t = cost(1 - cos 2t) + sin2t.sin t = 4sin2t.cos t
Y = sin t + sin 3t = sint(1 + cos 2t) + sin 2t.cos t = 4cos2t.sin t
C'est bien notre quadrifolium avec a = 4.
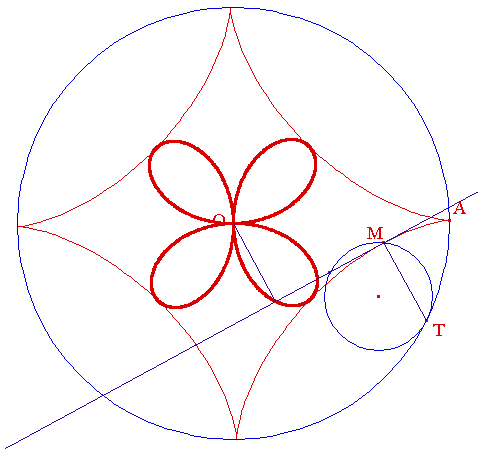
Génération du quadrifolium :
La podaire est générée ci-dessous au moyen d'un logiciel de géométrie dynamique, ici Cabri Géomètre, dans sa version CabriJava pour Internet :

Si votre navigateur accepte les applets
Java
(»
extension CheerpJ![]() ) :
) :
Pour effacer / relancer le lieu
double-cliquer, cliquer dans la figure.
Vous pouvez aussi déplacer T manuellement.
La normale en M est (TM)
Un pentafolium ?.. : »