Variables aléatoires discrètes       » Variable de Bernoulli | Loi binomiale | Loi de Pascal | Loi de Poisson | Loi faible des grands nombres | Autres lois

Dans un espace probabilisé fini Ω = {e₁, e₂, ..., e_n} de cardinal n, à toute éventualité e_i on peut associer un nombre réel x_i : on définit ainsi une application surjective X de Ω dans {x₁, x₂, ..., x_n}⊂R, appelée variable aléatoire (du latin alea = dé (jeu-de) = chance = hasard).

La loi de probabilité (on dit aussi distribution de probabilité) de la variable aléatoire X est l'ensemble des couples (x_i, p_i) où p_i = Prob{X = x_i} désigne la probabilité de réalisation de l'événement {X = x_i}.

• Cette loi de probabilité s'interprète comme l'application de {x₁, x₂, ..., x_n} dans [0,1] définie par x_i →Prob{X = x_i}.

On parle ici de variable aléatoire X discrète pour signifier que X ne prend qu'un nombre fini ou dénombrable de valeurs. Lorsque X peut prendre toute valeur d'un intervalle J de R avec une probabilité bien définie, on parle d'une variable aléatoire continue ou, plus justement, absolument continue.

Variables aléatoires continues :  »

Fonction de répartition :    

Dans un problème statistique, on cherche généralement la probabilité qu'une variable aléatoire X soit inférieure ou supérieure à une valeur donnée, ou encore comprise entre deux valeurs données (fourchette). On définit alors sa fonction de répartition F définie de R sur [0,1] par :

F(x) = Prob{X ≤ x}

C'est une fonction cumulative : si les x_i sont rangés par valeurs croissantes, alors :

• pour tout x < x_o, F(x) = 0

• F(x_o) = Prob{X = x_o}

• F(x₁) = Prob{X = x_o} + Prob{X = x₁}

• ...

• F(x_k) = Prob{X = x_o} + ... + Prob{X = x_k}

• F(x_n) = 1

• pour tout x > x_n, F(x) = 1

Exemple :    

Ci-dessous est représentée la fonction de répartition de la variable X définie par le lancement d'un dé (6 faces numérotées de 1 à 6) conduisant à un gain relatif de : -1 € si le 1 sort  | -2 € si tout autre numéro impair sort | +3 € si le 6 sort | +2 € si tout autre numéro pair sort :

   

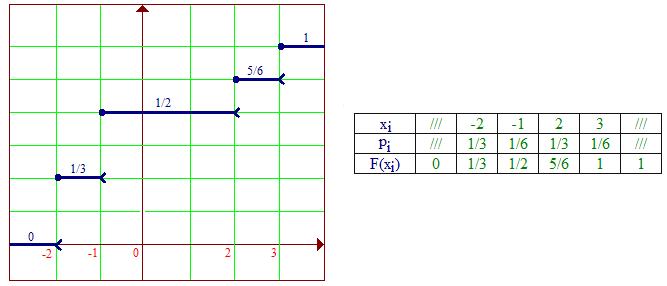
Sur le graphique et selon la coutume, le point (•) signifie une valeur prise effectivement par F, la pointe de flèche inversée signifiant le contraire : F est continue à droite en chaque x_i.

Médiane :   

De façon similaire à la médiane d'une série statistique, la médiane d'une variable aléatoire X discrète (ou continue) est la valeur m_d de X pour laquelle la fonction de répartition est égale à 1/2 :

F(m_d) = Prob(X ≤ m_d ) = 1/2

 ➔  Concrètement, il y a "autant de chances" de "voir se réaliser  l'événement X ≤ m_d ou son contraire. Comme en statistique, compte tenu du cas discret, on peut être amené à un calcul moyen lorsqu'aucun x_i ne fournit "exactement" F(x_i) = 1/2. Dans l'exemple ci-dessus, la médiane est -1.

Espérance mathématique (ou moyenne), variance et écart-type d'une variable aléatoire discrète :   

Tout comme l'on définit la valeur moyenne d'un caractère d'une série statistique comme moyenne pondérée de ses valeurs par leurs fréquences, ces dernières sont ici remplacées, on peut s'en douter, par les probabilités. C'est à Pascal que l'on doit cette notion dans son traité du Triangle arithmétique. On note généralement E(X) ce nombre :

E(X) = Σ x_i × Prob(X = x_i)

La variance de X est la moyenne des carrés des écarts par rapport à sa moyenne. L'écart-type de X est la racine carrée de sa variance.