ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
» En exemple : cas de la fonction sinus |
Interpolation polynomiale :
Soit f une fonction numérique. Interpoler f par un polynôme sur un intervalle [a,b], c'est choisir une subdivision, non nécessairement régulière :
et rechercher un polynôme P de degré n, dit polynôme d'interpolation, qui coïncide avec f en chaque point xi.
➔ On parle d'interpolation linéaire lorsque le polynôme est de degré 1 : l'arc de courbe est remplacé par un segment.
∗∗∗
Dans le cas de l'interpolation linéaire, on remplace l'arc de courbe (MaMb)
par le segment [MaMb].
Écrire y = P(x) en fonction de xo = a et x1 = b.
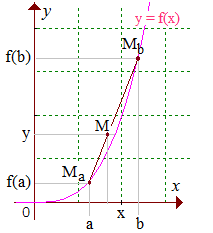
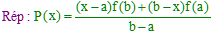
Plus généralement :
La fonction f étant seulement connue par un ensemble fini de points (nuage), Mi(xi , yi) , yi = f(xi) , a = xo, b = xn, interpoler f sur l'intervalle [a,b] par une fonction g de type donné (polynomial, logarithmique, exponentielle, trigonométrique, ...) consistera à calculer les paramètres de g afin d'approcher au mieux les valeurs connues des yi = f(xi).
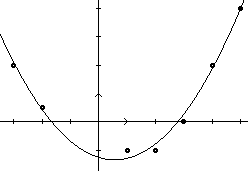
➔ Le cas se rencontre couramment en statistique. Au lieu d'interpolation, on utilise plus volontiers le terme statistique de régression, du latin regressio = retour, pour exprimer l'idée d'un retour à la source (le principe au sens logique) du nuage observé (qui en est la conséquence).
Une méthode de régression très utilisée est la méthode des moindres carrés : »
Historiquement, on a cherché à développer la fonction à approcher au moyen de polynômes jouissant de propriétés remarquables au sein d'espaces vectoriels euclidiens (espaces de Hilbert, espaces de Banach) :
et l'on démontre que, eu égard à la norme utilisée, le choix de zéros xi équirépartis pour des polynômes évoqués ci-dessus conduisent à la meilleure interpolation sur l'intervalle considéré. Dans le cas polynomial, Lagrange a proposé le polynôme suivant dit polynôme d'interpolation de Lagrange qu'utilisèrent auparavant Newton et Cotes (son élève) pour l'intégration approchée :
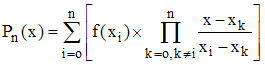
On vérifie que l'on a bien Pn(xi) = f(xi). P est donc une approximation polynomiale de f. Mais de gros écarts peuvent être constatés. La fonction f doit donc être assez régulière sur l'intervalle considéré.
Dans le cas de l'interpolation linéaire, nous retrouvons le résultat proposé en exercice ci-dessus :
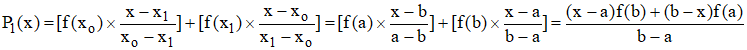
Méthode de Newton-Cotes pour l'intégration numérique : » Méthode de Simpson, dite des 3/8 : »
Outre la méthode des moindres carrés, des méthodes de régression plus subtiles permettent d'améliorer l'approximation afin de minimiser pour une distance bien choisie la différence entre f et Pn : on entre dans de subtils problèmes d'analyse fonctionnelle non développés dans cette chronologie. Les plus connues sont celles de Newton, de Gauss, de Bessel et l'approximation uniforme de Stone-Weierstrass.
| Interpolation de la fonction sinus par la méthode de Lagrange : |
A titre d'illustration simple de l'interpolation polynomiale de Lagrange, nous allons interpoler la fonction sinus sur l'intervalle [0,π] en utilisant tout d'abord trois points équidistants xo = 0, x1 = π/2, x2 = π. On a donc ici f(x) = sin x, n = 2 et :
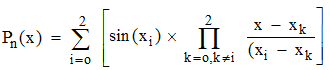
|
|
|
|
|
|
|
|
|
|
Dans ce cas très simple, les termes de rang 0 et 2 sont nuls. Reste à calculer le seul terme de rang 1 :
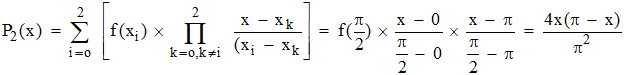
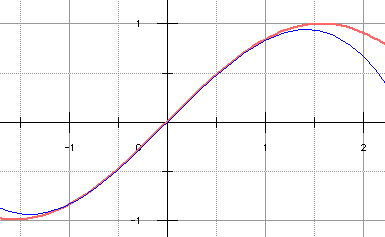
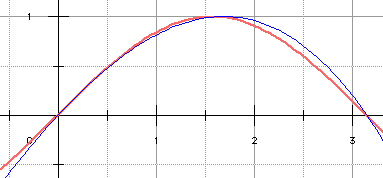
Ci-dessous, en rose épais, la fonction sinus et en bleu l'approximation P2 de Lagrange. Pas mal...
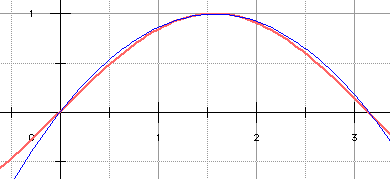
y = sin x en rose
et y = P2(x) en bleu
Affinons en ajoutant le point d'abscisse π/6 car c'est au voisinage de ce point que l'écart semble le plus grand :
|
|
|
|
|
|
|
|
|
|
|
|
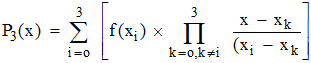
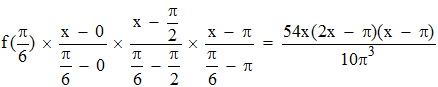
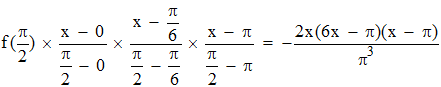
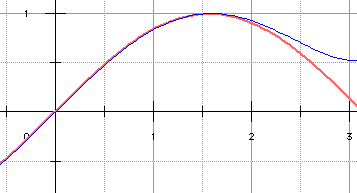
Ce qui fournit :
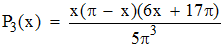
y = sin x en
rose
et y = P3(x) en bleu
:
On constate une amélioration
sensible sur [0,π/2]
mais on a cassé la symétrie
et aggravé l'erreur sur [π/2,π]
![]()
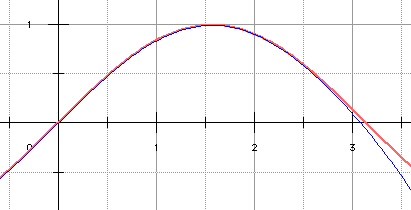
Et si le cœur
vous en dit, rajoutez le point d'abscisse
5π/6
mais la
méthode d'interpolation de Lagrange a un gros
défaut : si on ajoute un point, il faut tout
recalculer pour passer de Pn à
Pn+1. Celle de Newton conserve les coefficients du
polynôme Pn car le système calculant
les coefficients est triangulaire.
Connaissant le développement en série de sin x : sin x = x - x3/3! + x5/5! - x7/7! + ... on obtient des approximations plus simples et plus précises :