ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Les mathématiques sont-elles une science ?  et l'informatique ?            » Mathématique & Informatique | Les maths : ça sert à quoi ? | Petite chronologie des PC

Tout d'abord il s'agit de préciser ce que l'en entend par science : l'inévitable Petit Larousse Illustré la définit ainsi : « du latin scire = savoir. Ensemble organisé de connaissances relatives à certaines catégories de faits ou de phénomènes ».

Dans ces conditions, l'affaire est entendue, l'informatique n'est pas une science !

 ➔  Le terme informatique, dû à Philippe Dreyfus, ingénieur chez Bull, date de 1962. L'appellation fut très appréciée par l'Académie française qui  l'admit officiellement en 1967 pour signifier science du traitement de l'information : tikôs en grec, signifie qui se rattache à, qui est propre à, et tekhnê signifie étude, science. La mathématique, quant à elle, au sens des grecs anciens, est la discipline qui s'apprend (du grec manthanein = apprendre) : entendons-là, la discipline que chacun "devrait" apprendre...

Avec Claude Bernard, nous pouvons définir la science comme une discipline ayant pour but l'explication d'une catégorie de phénomènes susceptibles de se répéter à l'identique. La science se fonde sur l'observation puis l'expérience, laquelle est une observation provoquée.

La démarche scientifique selon Claude Bernard

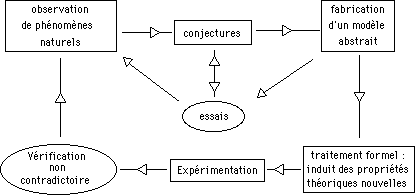Avec cette acception, on peut affirmer :

• qu'il n'y a pas de science du fait isolé, non répétitif : en ce sens l'histoire n'est pas une science;

• que la science recherche des lois (rapports nécessaires et constants entre les phénomènes, élabore des modèles (atome de Bohr, l'Univers selon Albert Einstein) :

  - La physique, la chimie, la biologie sont principalement des sciences expérimentales.
  - L'astronomie est une science de l'observation ainsi que la psychologie, la sociologie.

Si la science est ainsi entendue, la mathématique n'en est pas une : même si, dans certaines branches, elle se base sur l'observation (par exemple, les axiomes de la géométrie euclidienne) elle ne prétend pas en déduire une explication des phénomènes observés. La mathématique s'échappe du réel, elle peut bâtir des univers abstraits, et à priori absurdes, comme la géométrie de Lobatchevski. La mathématique crée des théories reposant on non sur la réalité et, plus récemment, recherche des modèles de ses théories.

Afin de récupérer les mathématiques comme une science, on peut admettre qu'une telle notion peut ne pas être directement orientée vers des fins pratiques, c'est pourquoi l'on emploie souvent les expressions science pure ou science fondamentale par opposition aux sciences appliquées qui ne sont autres que des techniques reposant sur une science.

Ceci dit, une certitude, malgré les attaques médiatico-politiques d'un ancien ministre de l'Éducation Nationale, il n'y a pas de science sans mathématiques. Les mathématiques sont l'outil et, dans une large mesure, le langage des sciences de l'école (d = v × t) à l'université (E = mc²). Et c'est dans cet esprit qu'elles devraient être enseignées depuis l'abandon de l'enseignement des mathématiques dites « modernes » introduit au tout début des années 1970. Il n'en est hélas rien !

Une technique peut se définir comme un ordre d'activités tendant à des fins pratiques : il s'agit non plus de décrire et connaître note univers mais plutôt de le modifier. Pour ce faire, une technique ne procède pas nécessairement de la science : l'homme a travaillé les métaux, fabriqué des alliages ou obtenu du vin en dehors de toute connaissance de chimie et encore aujourd'hui, nombre de techniques reposent sur une part d'empirisme et peuvent être le fruit d'approximations successives.

Cependant, ne serait-ce que par désir d'efficacité et d'économie (rentabilité), les techniques élaborées sont fondées sur les sciences. Ainsi une technique est aussi un savoir, un objet d'étude, une discipline. Et pour désigner cet aspect non empirique d'une technique, on parle de technologie.

Mais qu'en est-il de l'informatique ? Elle est sans nul doute un ensemble organisé de connaissances. Elle ne procède cependant pas de l'observation des phénomènes, ni de l'expérience : ne pas confondre expérience et tests (ou essais) tendant à prouver qu'un programme informatique n'est pas faux. Elle ne formule pas de lois et ne propose aucun modèle du monde extérieur.

Ainsi, l'informatique est plutôt une technique, un ordre d'activités tendant à des fins pratiques : traitement logique et automatique de l'information faisant appel à la logique mathématique. Par là, c'est aussi un savoir, un objet d'étude, une technologie au service des sciences et des techniques de toute nature, une science au sens large : qualifions la alors, pour conclure, de science appliquée.

Démarche scientifique et problème ouvert en pédagogie : »        Théorie des modèles : »