
ChronoMath,
une chronologie des MATHÉMATIQUES
à l'usage des professeurs de
mathématiques, des étudiants et des élèves des lycées & collèges
On résout ici, en nombres entiers,
une équation de la forme :
(e) ax
+ by = c
où a, b et c sont des
entiers donnés non nuls.
➔
Le cas c = 0 est trivial :
x = -bk, y = ak, k décrivant Z.
Dans ce programme :
- Selon la
théorie, le
PGCD de a et b doit diviser c, sinon il n'y a pas de
solutions.
- l'entier a doit être impérativement
positif;
- b peut être
négatif : le programme calcule avec b positif puis
change y en -y;
- c peut être
négatif.
Avec cette petite restriction relative au coefficient a,
une équation comme -3x + 7y = 5 devra être transformée en 3x - 7y = -5 puisque
le programme accepte des coefficients b et c négatifs.
➔
Le programme recherche le
PGCD d des entiers a et b et donne une solution particulière (xo,yo),
en résolvant l'identité de Bézout. Selon l'étude théorique (cliquez sur la clé
en en-tête), la solution générale est alors :
xo - b' k ,
yo +
a'
k ,
yo +
a' k, avec a' = a/d,
b' = b/d, k décrivant Z
k, avec a' = a/d,
b' = b/d, k décrivant Z
|
<SCRIPT
LANGUAGE=JavaScript>
var a,b
function go()
{
a="" ; a=prompt("a = ",a)
if (a==null) {return}
a=eval(a)
if (a< 0) {alert("a doit être
positif"+"\n"+"Recommencez...")}
b="" ; b=prompt("b = ",b)
if (b==null) {return}
b=eval(b)
sb=1;if(b< 0) {b=-b;sb=-1}
c="" ; c=prompt("c = ",c)
if (c==null) {return}
c=eval(c);
aa = a ; bb = b ; cc = c;
gcd=pgcd()
if (c % gcd != 0)
{alert("pgcd("+a+" , "+b+") = "+gcd+"\n"+ gcd+ " ne divise
pas "+c+"\n"+" Pas de solutions")
}
else
{
a=aa/gcd ; b = bb/gcd ; c = cc/gcd ; n=0 ; rn = 0
while (rn != 1)
{
n++
an=n*a ; rn = an % b ; qn = (an-rn)/b
}
u=n ; v = -qn;
alert("pgcd("+aa+" , "+bb+") = "+gcd+"\n"+a+"*"+u+" +
"+b+"*("+v+") = 1"+"\n"+
"Une solution est :"+"\n"+"xo =
"+u*c+" , yo = "+ v*c*sb)
}
return
}
//------on utilise
ci-dessous algorithme
d'Euclide pour le pgcd
function pgcd()
{
while (b > 0)
{
r = a % b
a = b
b = r
}
return a
}</SCRIPT>
|
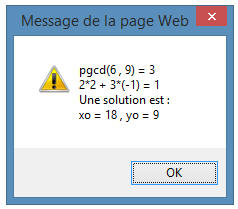
Un exemple d'exécution :
-
6x - 9y = 27; l'équation est équivalente à
2x - 3y = 9 en divisant par d = 3, pgcd de a et b
divisant c. L'ordinateur cherche alors à satisfaire l'identité de
Bézout et obtient 2 × 2 + 3 × (-1) = 1. En multipliant par 9, on a : 2
× 18 + 3 × (- 9) = 9 pouvant s'écrire :
2 × 18 - 3 × 9 = 9 : une solution est xo =
18, yo = 9
La solution générale est alors x = 18 +
3k, y = 9 + 2k.
© Serge Mehl -
www.chronomath.com


![]() k ,
yo +
a'
k ,
yo +
a'![]() k, avec a' = a/d,
b' = b/d, k décrivant Z
k, avec a' = a/d,
b' = b/d, k décrivant Z