
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
» Programme JavaScript | Exercice |
On se propose de calculer n! (factorielle de n) au moyen d'un tableur en utilisant une procédure fonctionnelle : cellule faisant appel à elle-même : c'est une procédure récursive, puis, s'aidant d'un programme élémentaire, de comparer les calculs à l'approximation de De Moivre et Stirling :
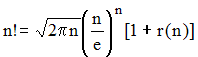
où r(n) tend vers 0 lorsque n tend vers l'infini.
| Programmation de la formule : |
On passe en mode dit itératif autorisant les références circulaires (récursion) et plutôt que d'indiquer à chaque fois à l'ordinateur le nombre d'itérations, nous allons créer notre propre compteur et test d'arrêt.
La ligne 1 sert aux dénominations des cellules de la ligne 2.
Noms des cellules : L2C1 est n ; L2C2 est k (récursion); L2C3 est fac = n! (récursion); L2C4 est d.
En A2 (L2C1) : on donne n.
En D2 (L2C4) : on crée un drapeau d valant 0 ou 1 permettant d'initialiser les calculs (d=0) et de lancer le calcul (d=1).
En B2 (L2C2) : on crée le compteur k. Si d = 0, k est mis à 1, sinon on l'incrémente tant qu'il ne dépasse pas n. Sinon, k prend sa valeur précédente, donc n+1 : ce qui le stoppe.
En C2 (L2C3) : on définit fac qui à chaque itération vaut k! : tant que k ≤ n, fac = fac*k, sinon fac prend sa valeur précédente, donc n!, et le procédé est stoppé :
| A |
B |
C |
D |
|
|
|
n |
|
|
|
|
|
10 |
|
|
|
| Exemple d'exécution : |
| A | B | C | D | |
|
|
n |
|
|
|
|
|
10 |
|
|
|
| Factorielle n et la formule de Stirling |
On écrit ici un programme simple calculant n! avec en regard l'approximation de Stirling et l'erreur relative commise par cette approximation.
En A2 : on initialise n à 1
En A3 : on incrémente n et on recopie ensuite vers le bas.
En B2 : on initialise n! à 1
En B3 : on écrit que n! = n que multiplie (n-1)! et on recopie vers le bas.
En C2 : c'est la formule de Stirling. Le nombre π = 3,1415926535... est une fonction du tableur (ici EXCEL) qui est obtenu en tapant PI().
En D2 : le calcul de l'erreur relative commise par l'approximation Sn de Stirling, àsavoir : en = | n! - Sn | / n!
|
|
|
|
|
|
|
1 |
n |
|
|
|
|
2 |
=1 |
=1 |
=RACINE(2*PI()*A2)*((A2/EXP(1)))^A2 |
=ABS(B2-C2)/B2 |
|
3 |
=A2+1 |
=A3*B2 |
=RACINE(2*PI()*A3)*((A3/EXP(1)))^A3 |
=ABS(B3-C3)/B3 |
|
4 |
=A3+1 |
=A4*B3 |
=RACINE(2*PI()*A4)*((A4/EXP(1)))^A4 |
=ABS(B4-C4)/B4 |
|
5 |
... |
... |
... |
... |
Pour n "grand", l'important est d'avoir une erreur relative en "faible" : la formule de Stirling semble très satisfaisante :
| A | B | C | D |
| n | n! "exact" selon Excel... | n! selon Stirling | err.rel. |
| 1 | 1 | 0,922 | 7,79% |
| 2 | 2 | 1,919 | 4,05% |
| 3 | 6 | 5,836 | 2,73% |
| 4 | 24 | 23,506 | 2,06% |
| 5 | 120 | 118,019 | 1,65% |
| 6 | 720 | 710,078 | 1,38% |
| 7 | 5040 | 4980,396 | 1,18% |
| 8 | 40320 | 39902,395 | 1,04% |
| 9 | 362880 | 359536,873 | 0,92% |
| 10 | 3628800 | 3598695,619 | 0,83% |
| 11 | 39916800 | 39615625,051 | 0,75% |
| 12 | 479001600 | 475687486,473 | 0,69% |
| 13 | 6227020800 | 6187239475,193 | 0,64% |
| 14 | 87178291200 | 86661001740,599 | 0,59% |
| 15 | 1307674368000 | 1300430722199,470 | 0,55% |
| 16 | 20922789888000 | 20814114415223,100 | 0,52% |
| 17 | 355687428096000 | 353948328666101,000 | 0,49% |
| 18 | 6402373705728000 | 6372804626194310,000 | 0,46% |
| 19 | 121645100408832000 | 121112786592294000,000 | 0,44% |
| 20 | 2432902008176640000 | 2422786846761140000,000 | 0,42% |
| 21 | 51090942171709440000 | 50888617325509700000,000 | 0,40% |
| 22 | 1124000727777607680000 | 1119751494628240000000,000 | 0,38% |
| 23 | 25852016738884976640000 | 25758525370529300000000,000 | 0,36% |
! En fait, la précision d'Excel est dépassée pour n > 20 et le résultat affiché en colonne B pour n > 20 est donné par le programme Derive, logiciel de calcul formel, intégré à la calculatrice TI92 de Texas Instruments. Excel fournit en effet :
21! = 51090942171709400000 22! = 1124000727777610000000 23! = 25852016738885000000000
et aggrave son cas au-delà, tout en diminuant malgré tout l'erreur relative, ce qui ici importe plus que l'exactitude : sa précision étant de 16 chiffres significatifs, Excel ajoute des zéros intempestifs.