factorielle multiprécision

ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Calcul multiprécision de n! Version JavaScript
» Version récursive , version BASIC

Rappelons que la notation n!, factorielle n , désigne le produit des n premiers entiers naturels non nuls :

n! = 1 × 2 × ... × n

Le problème, dans le calcul de n!, est la très rapide croissance de ce célèbre produit. En dehors d'un calcul manuel et laborieux, on obtiendra généralement :

avec une calculatrice : une dizaine de chiffres significatifs
avec un micro-ordinateur : 15 à 16 chiffres significatifs (double précision)

Quelques machines spécialisées dans le calcul formel et certains logiciels mathématiques onéreux (Derive, Mapple, Mathematica) fourniront, à la demande, un nombre important de chiffres significatifs. L'objectif est ici de faire aussi bien.

Le procédé est très simple : il suffit de travailler dans une base élevée, nous choisissons ici 10000, et de mettre en place l'algorithme de division dans cette base, calquée sur celle de la division en base 10. Cet algorithme est utilisé dans les calculs précis des nombres π et e décrits dans ChronoMath :

300 décimales (ou plus) de π : » 300 décimales (ou plus) de e : »

Apprenons à l'ordinateur la multiplication d'un nombre entier par un nombre de 400 chiffres (digits) : le multiplicande Z est un entier possédant 400 digits, le multiplicateur est un entier "normal" m.

Si B est la base utilisée (ici B = 10000), Z est de la forme :

T_oBⁿ+ T₁B^n-1+ ... + T_n-2B² + T_n-1B + T_n

Les T_i, pour i variant de 0 à n = 100, sont les chiffres (tranches à 4 chiffres en base 10) de notre système à base B. On effectue la multiplication par m de "droite" à "gauche" :

T_n devient T_nB que l'on écrit sous la forme B.q + r en effectuant une division euclidienne. Par suite, le dernier "chiffre" est maintenant T_n = r;
on repousse alors Bq dans BT_n-1 qui devient B(T_n-1 + q);
T_n-1 + q est multiplié par m que l'on écrit sous la forme Bq' + r';
B(T_n-1 + q) devient alors B(Bq' + r') = B²q' + Br'. Par suite l'avant dernier "chiffre" T_n-1 est maintenant r'.
Et ainsi de suite...

Le cas de la multiplication de T_o est particulier : il doit être multiplié par m et hériter du dernier quotient q. Un risque de dépassement peut exister : u ne doit pas dépasser 9999. Si le dépassement a lieu, il nous faut une tranche supplémentaire : il y a un dépassement de capacité. Le programme ci-dessous affiche également la valeur approchée de n! au moyen de la formule de Stirling :

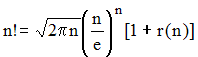
avec r(n) = 1/12n + 1/288n² + o(1/n³)

» Formule de Stirling

! le dépassement de capacité a lieu pour pour n > 212 !
Les tranches étant dimensionnées à 100, on a au total 101 tranches de 4 chiffres, soit 404 digits.
La formule d'approximation de Stirling est "out" au-delà de n = 170...

<SCRIPT LANGUAGE=JavaScript>

function go()
{
b=10000;t=new Array(100)
for (i=0;i<=100;i++) {t[i]=0} // mise à zéro des tranches
var n=""; // la dernière tranche contiendra n
n=eval(prompt("Entrez un nombre:",n))
t[100]=n
for(m=n-1;m>=2;m--)
{q=0
for (i=100;i>=1;i--){p=t[i]*m+q;r=p%b;q=(p-r)/b;t[i]=r}
t[0]=t[0]*m+q
}
if (t[0] > 9999) {alert("depassement de capacite")}
j=0
while (t[j]==0) {j++}    // on n'affiche pas les premières tranches nulles
aff=t[j].toString()
for(i=j+1;i<=100;i++)
{
if (t[i]< 10) {aff=aff+"0"}
if (t[i]< 100) {aff=aff+"0"}
if (t[i]< 1000) {aff=aff+"0"}
// si une tranche ne possède pas 4 chiffres, il faut ajouter des zéros devant.
// par exemple, si une tranche vaut 37, en fait, elle vaut 0037
aff=aff+t[i].toString() // conversion des tranches en chaînes
}
stir=Math.sqrt(2*Math.PI*n)*Math.pow(n/Math.exp(1),n)+1/(12*n)+1/(288*n*n)
stir=Math.ceil(stir)
alert(n+"!="+aff+"\n"+"\n"+n+"! stirling ="+stir)
}
</SCRIPT>

Calcul de 30!

Calcul de 100!

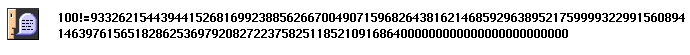
Calcul de 200!

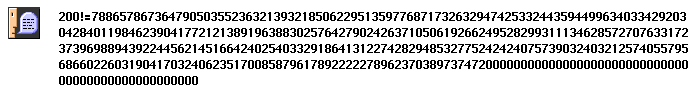
n!, problème du représentant de commerce et conjecture P = NP : »

© Serge Mehl - www.chronomath.com