ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

L'exponentielle complexe     »  cas réel | logarithme complexe

Afin de s'assurer de la dérivabilité de la fonction  z → ez pour z complexe, le plus simple est de faire comme Euler en posant :

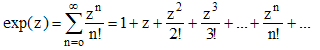
Le nombre complexe exp(z) est alors bien défini pour tout z de C car la règle de d'Alembert pour les séries entières nous assure que la série ci-dessus est absolument convergente.

Soit K⊂C un disque de rayon r, on alors | zn/n! | ≤ rn/n! ce qui prouve la convergence normale de notre série sur tout disque de C. Un résultat de Weierstrass exprime que la convergence normale entraîne la convergence uniforme car C est complet et le même Weierstrass nous indique que les zn/n! étant continues, il en est de même de la somme de la série : notre fonction z → exp(z) est continue en tout point de C.

 ➔  Tout comme pour l'exponentielle dans le cas réel, on démontrerait très facilement que :

exp(z + z') = exp(z) x exp(z')    (1)

Maintenant nous aimerions que z → exp(z) soit dérivable : dans C, on parle de fonction holomorphe. Pour cela, on peut dériver notre série terme à terme car les conditions sont remplies, ce qui montre que z → exp(z) est dérivable et identique à sa dérivée sur C tout entier. On peut aussi très simplement remarquer avec J. Lelong-Ferrand et J.M. Arnaudiès que l'on peut s'écrire :

La fonction φ est manifestement continue (même raison que pour exp). Sa limite en 0 est donc φ(0) = 1/2 et on a alors le résultat :

Le nombre dérivée en z de la fonction exp est la limite pour h tendant vers 0 dans C du taux (exp(z + h) - exp(z))/h. Avec l'aide de la formule (1) La mise en facteur de exp(z) conduit immédiatement au résultat espéré :

[exp(z) ]' = exp(z)       (2)

Si z est un réel x, notre fonction coïncide avec la fonction exponentielle x → ex . Si z est imaginaire pur, z = it, on constate que la partie réelle est le développement en série de cos t et la partie imaginaire est le développement de sin t : exp(it) = cos t + i.sin t, on retrouve donc la formule d'Euler eit = cos t + i.sin t.

Arrêtons là le suspense :                

Notre fonction exp qui coïncide sur R avec la fonction exponentielle x → ex est encore notée ez dans C : c'est la fonction exponentielle complexe. Il s'agit ainsi d'une fonction holomorphe sur C tout entier (fonction analytique).

Le logarithme complexe :

Cette introduction au logarithme complexe est proposé en exercice :

a) En posant z = r(cost + i.sint) où r est le module de z et t  un argument, montrer que la fonction z →ez est périodique de période 2iπ.

b) On assimile tout complexe z = x + iy à un couple (x,y) de R x R.
Prouver que la restriction f de l'exponentielle complexe à U =  R x ]-π,π] est une bijection de U sur C \ R-.

c) Exprimer la fonction réciproque de f.   Rép : f -1(z) = ln |z| + i.Arg z, avec Arg z = argument principal de z.

d) On note désormais Log la fonction f-1 : on a donc Log ez = z. Retrouver que Log z est holomorphe (dérivable) sur C \ R-

z → Log z = ln |z| + i.Arg z est appelé logarithme népérien principal de z.

 !
Si on n'y prend pas garde, cette fonction pose de sérieux problèmes de continuité...

Racine carrée complexe, Logarithme complexe et surfaces de Riemann : »              Intégrale complexe : »

 ➔   Pour en savoir plus :

© Serge Mehl - www.chronomath.com