
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
» Étude de la cycloïde , étude analytique de la développée , développante de la cycloïde |
 |
Rappelons que la développée d'une courbe est l'enveloppe de ses normales. Engendrer la développée de l'ellipse est chose aisée grâce au logiciel CabriJava. La cycloïde est obtenue par roulement. A chaque instant, la normale est définie par la droite (TM) où T est le point tangent à la droite sur laquelle roule le cercle (point instantané de rotation), et M le point correspondant de la cycloïde :
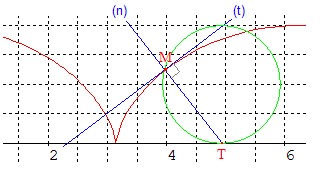
Génération :
La cycloïde est générée ci-dessous au moyen du logiciel de géométrie dynamique Cabri Géomètre, dans sa version CabriJava pour Internet :
la figure animée ci-dessous trace les normales, on voit se former la développée en tant qu'enveloppe. La développée semble être une cycloïde isométrique.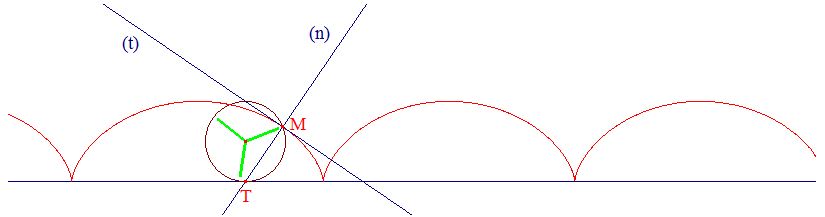

Si votre navigateur accepte les applets
Java
(»
extension CheerpJ![]() ) :
) :
Génération de la
développée de la cycloïde
: pour effacer/relancer le lieu
double-cliquer
Vous pouvez déplacer T manuellement pour observer le phénomène...
Ci-dessous, le logiciel a tracé la développée de la cycloïde ci-dessus. C'est manifestement une cycloïde isométrique ! Vous pouvez le prouver en utilisant l'équation générale d'une développée. On observe que la normale en chaque point M est la tangente en chaque point de la développée.
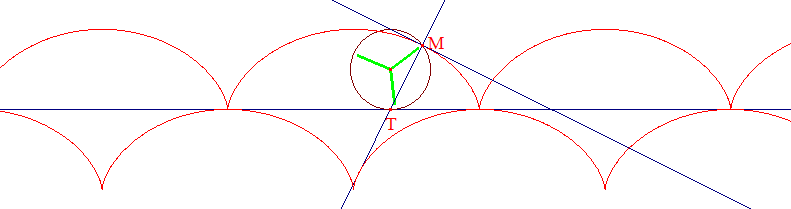

Si votre navigateur accepte les applets
Java
(»
extension CheerpJ![]() ) :
) :
Génération de la
développée de la cycloïde
: pour effacer/relancer le lieu
double-cliquer
Vous pouvez déplacer T manuellement pour observer le phénomène... :