Développée de la cycloïde

ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Développée de la cycloïde ••• animation
» Notion de développée d'une courbe , pendule de Huygens

On sait que la cycloïde est le lieu du point d'un cercle de rayon r qui roule, sans glisser sur une droite. son équation paramétrique est :

x = r(t + sin t) et y = r(1 + cos t)

Les résultats concernant l'étude générale de la développée d'une courbe plane, fournissent facilement l'équation de sa développée :

X = r(t - sin t) , Y = -r(1 + cos t)

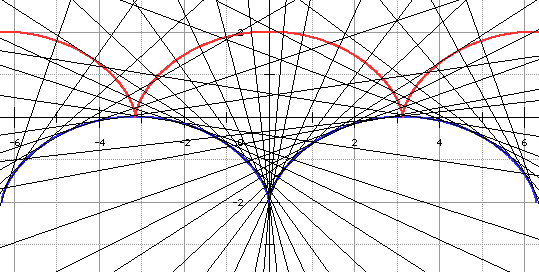
on voit ici la développée (en bleu), enveloppe des normales à la cycloïde d'origine (en rouge)

C'est donc une cycloïde isométrique (Huygens fut le premier à le constater) : on voit que l'on peut l'obtenir par la translation (x,y) → (x + π, y - 2r) : en effet, la courbe image de la cycloïde aura alors pour équation :

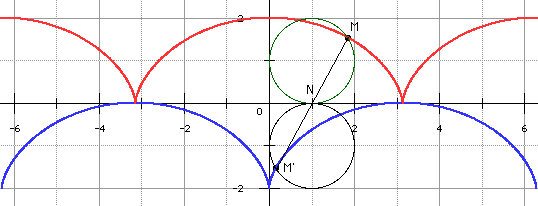
X = r(t + sin t) + π = r[t + π - sin(t + π)] = r(u - sin u) en posant u = t + π

Y = r(1 + cos t) - 2r = -r - cos(t + π) = -r(1 + cos u).

➔ On peut retrouver la développée de la cycloïde sans calculs si l'on sait que le rayon de courbure est, en chaque point de la cycloïde, le double de la sous-normale, soit, ci-dessous, le double de MN. Le symétrique M' de M par rapport à N, est le centre de courbure de la cycloïde au point M : il décrit donc la développée.

Représentons alors, à chaque instant, le symétrique (c') du cercle roulant par rapport à (Ox) : il est clair que M' décrit la cycloïde obtenue lorsque (c') roule sur la parallèle à Ox, ici d'équation y = -2, soit, en général, y = -2r.

••• Animation : »