
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

 |
En architecture, on rencontre des formes d'apparence elliptique qui sont en fait en "anse de panier", assemblage d'arcs de cercles ayant la même tangente aux points de jonction. Une telle forme ne résulte pas, comme l'ovale, d'une courbe mathématique usuelle. On pourrait bien sûr en donner une équation cartésienne par morceaux mais cela n'aurait guère d'intérêt.

Abbaye
de Fontfroide, X1e siècle (Pyrénées orientales)
Nom de la courbe : anse de panier. C'est aussi un demi-ovale elliptique.
Étymologie : du latin ansa = anse (même sens).
Définitions fonctionnelles possibles : néant...C'est un assemblage géométrique d'un nombre impair d'arcs de cercle (trois le plus généralement).
Applications : architecture, voûtes dites "surbaissées" de portes de châteaux & chapelles (Renaissance en particulier : château de Blois, aile Louis XII), de ponts, de tunnels, ... Notons que la voûte surbaissée est parfois réduite à deux quarts de cercle reliés à une horizontale.

Escalier du château de Hautefort (Corrèze).
| Construction de l'anse à 3 centres : |
Cette construction, très simple, fixe l'élévation (flèche) de la voûte lorsque l'ouverture (sa largeur), correspondant à AB ci-dessous, est donnée :
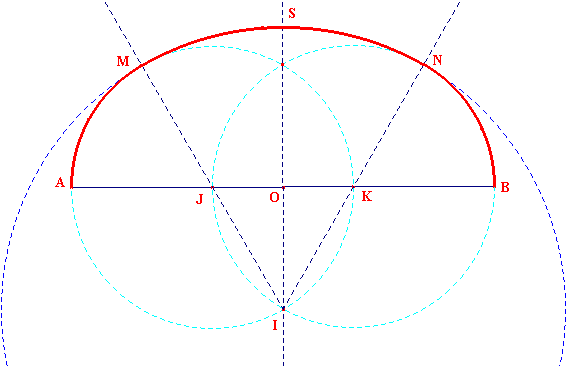
L'anse de panier est la ligne AMSNB (en gras rouge), belle voûte réunion des arcs AM, MN et NB. On notera que les cercles CJ, de rayon JA = JI, et CI, de rayon IM = 2JI sont tangents en M. De même CK est tangent en N à CI.

Anse de panier à 3 centres avec élévation et largeur variables :
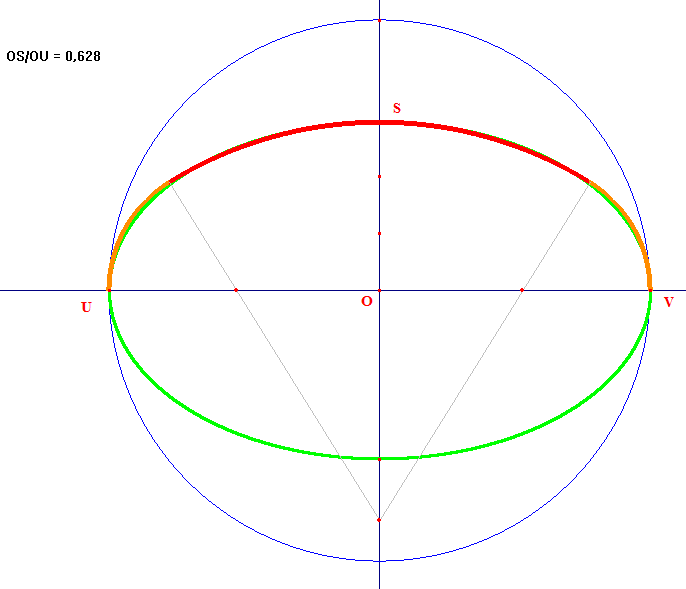
Voici la même figure que ci-dessus générée par le logiciel Cabri Géomètre :

Anses de panier à 5 et 7 centres : »