Anse de panier à 5 centres

ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Anse de panier à 5 centres » 3 centres , 7 centres , ovale & ove , voûte égyptienne

Tracer une droite horizontale. Placez sur la gauche un point U;
Reporter 5 segments de même mesure : UA = UV/5;
Tracer la médiatrice de [UV];
Reporter OJ = JC = UA;
Tracer la demi-droite [JA);
Le cercle de centre A passant par U coupe [JA) en B;
Ne conserver que l'arc UK;
Tracer la demi-droite [CB);
Le cercle de centre B passant par K coupe [CB) en L;
Ne conserver que l'arc KL;
Le cercle de centre C passant par L coupe la médiatrice en M;
Ne conserver que l'arc LM;
Compléter par symétrie.

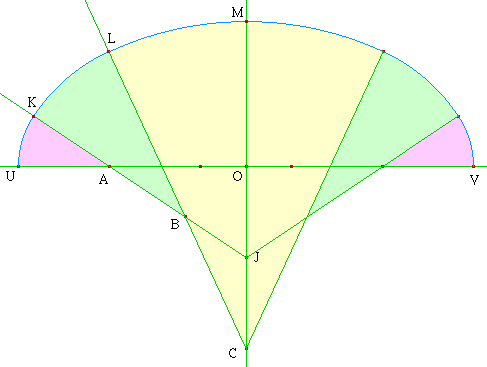
➔ On n'utilise bien que 5 centres car C est utilisé à gauche et à droite de l'axe de symétrie... On pourra vérifier par des considérations élémentaires que la somme des mesures des arcs égale 180° (mesure au sens de l'angle au centre) :

^UAK + ^KBL + ^LCM = 90°

C'est une propriété des anses de panier quel que soit le nombre d'arcs

Anse de panier à 5 centres avec élévation et largeur variables :

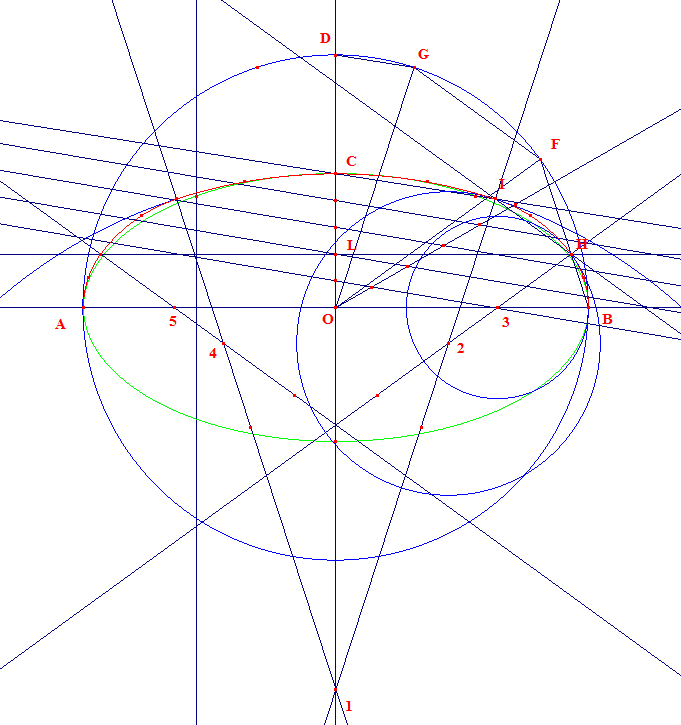
La même figure lorsque les constructions intermédiaires n'ont pas été cachées... :

Les figures ci-dessous, identiques aux deux précédentes, sont générées au moyen du logiciel de géométrie dynamique Cabri Géomètre, dans sa version CabriJava pour Internet :

Si votre navigateur accepte les applets Java (» extension CheerpJ) :
Vous pouvez déplacer les sommets B et C. En vert l'ellipse de demi-axes OB et OC. En bleu le cercle principal de l'ellipse.
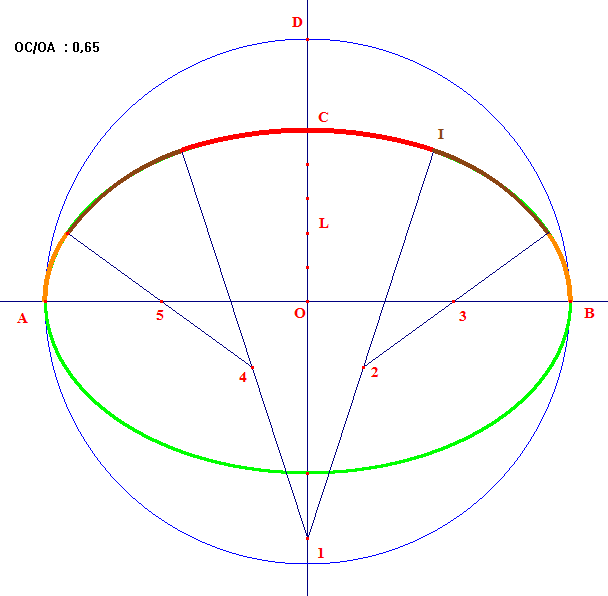
On remarquera la quasi parfaite concordance avec l'ellipse sous-jacente lorsque OC/OB ≃ 0,65.

et la même figure lorsque les constructions intermédiaires n'ont pas été cachées... :

Anse de panier à 7 centres :

La construction précédente se généralise à un nombre impair quelconque de centres : les centres successifs sont A, B, C et D. Et on complète par symétrie.