ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Anneau de Boole, algèbre de Boole et structure d'anneau   niveau Sup

1.  Montrons que tout anneau de Boole peut être muni de la structure d'algèbre de Boole en conservant sa multiplication, l'addition étant redéfinie par : x + y = (x ⊕ y) ⊕ (x ⊗ y).

On part d'un anneau de Boole (A,⊕,⊗,0,1) en conservant sa multiplication ⊗. La nouvelle addition, notée +, est définie par x + y = (x ⊕ y) ⊕ (x ⊗ y). Nous cherchons à prouver que (A,+,⊗,0,1) est une algèbre de Boole. Étudions point par point les propriétés à vérifier :

a/  Un anneau de Boole est commutatif : la multiplication est commutative. L'addition dans (A,+) est clairement commutative.

b/ La loi ⊗ est associative dans (A,⊗). Il nous faut montrer l'associativité de la nouvelle addition : pour tous x, y et z, a-t-on (x + y) + z = x + (y + z) ?

(x + y) + z = [(x ⊕ y) ⊕ (x ⊗ y)] + z = ([(x ⊕ y) ⊕ (x ⊗ y)] ⊕ z) ⊕ [(x ⊕ y) ⊕ (x ⊗ y)]⊗z

On développe et on réordonne en évitant les () inutiles :

(x + y) + z = x ⊕ y ⊕ z  ⊕ (x ⊗ y) ⊕ (y ⊗ z) ⊕ (z ⊗ x) + (x ⊗ y ⊗ z)

Vu la commutativité, plutôt que de calculer x + (y + z), on peut calculer (y + z) + x : on constate une permutation circulaire x → y, y → z, z → x. Si le calcul précédent est invariant dans cette permutation, alors c'est gagné. Or c'est le cas !

c/ La multiplication ⊗ doit être distributive sur la nouvelle addition + sachant que ⊗ est distributive sur ⊕. On a  :

x ⊗ (y + z) = x ⊗ [(y ⊕ z) ⊕ (y ⊗ z)] = (x ⊗ y) ⊕ (x ⊗ z) ⊕ (x ⊗ y ⊗ z)

Comparons à x ⊗ y + x ⊗ z = [(x ⊗ y) ⊕ (x ⊗ z)] ⊕ (x ⊗ y) ⊗ (x ⊗ z) = (x ⊗ y) ⊕ (x ⊗ z) ⊕ (x ⊗ x ⊗ y ⊗ z) : il s'agit du même résultat car dans l'anneau de Boole x ⊗ x = x.

d/ L'addition + doit être distributive sur la multiplication ⊗.
   Cela peut vous paraître bizarre, mais il nous faut montrer que x + (y ⊗ z) = (x + y) ⊗ (x + z)...

Le premier membre est tout simplement x ⊕ y⊗z + x⊗y⊗z. Le second est plus compliqué :

(x + y) ⊗ (x + z) = [(x ⊕ y) ⊕ (x ⊗ y)]⊗[(x ⊕ y) ⊕ (x ⊗ y)]

En utilisant que x ⊗ x = x, on obtient :

(x + y) ⊗ (x + z) = x + (x ⊗ z) ⊕ (y ⊗ x) ⊕ (y ⊗ z) ⊕ (x ⊗ z) ⊕ (x ⊗ y) ⊕ (y ⊗ x ⊗ z) ⊕ (x ⊗ y) + (x ⊗ y⊗ z) + (x ⊗ y⊗ z)

Mais dans l'anneau A, les éléments sont involutifs et la loi ⊗ est associative et commutative. Finalement, il vient :

(x + y) ⊗ (x + z) = x ⊕ y ⊗ z + x ⊗ y ⊗ z   CQFD

e/ 1 est neutre dans (A,⊗) et 0 est neutre dans (A,⊕). On remarque que x + 0 = (x ⊕ 0) ⊕ (x ⊗ 0) = x ⊕ 0 = x. La loi + étant commutative, on a x ⊕ 0 =  0 ⊕ x = 0 pour tout x : 0 est neutre dans (A,⊕).

f/ Le complémente x d'un élément x doit vérifier x + x = 1 et x ⊗ x = 0. Eu égard à cette dernière condition , la première relation s'écrit x ⊕ x = 1. C'est une équation dans le groupe (A,⊕). On ajoute x à gauche dans les deux membres et on obtient x = x ⊕ 1 comme unique solution et on vérifie que l'on a bien x + x = 1 et x ⊗ x = 0.

2. Inversement, vérifions qu'une algèbre de Boole peut être munie d'une structure d'anneau commutatif unitaire en conservant la multiplication, l'addition du groupe abélien sous-jacent étant définie par :

x ⊕ y = (x * y) + (x * y)

Notons (E,+,*,0,1) l'algèbre de Boole initiale. (E,⊕) doit être un groupe groupe abélien. La loi ⊕ est manifestement commutative et 0 est son élément neutre. Pour tout x, on a x ⊕ x = (x * x) + (x * x) = 0 + 0 = 0. Par conséquent, tout élément est symétrique de lui-même pour cette loi. Reste à montrer que la loi ⊕ est associative et que la multiplication * est distributive par rapport à cette addition.

 ➔   Les lois + et * étant commutatives et associatives, on évitera toute parenthèse inutile dans le calcul et on écrira des produits partiels dans l'ordre alphabétique. De plus, on utilise la convention pratique selon laquelle la multiplication est prioritaire sur l'addition et x*y s'écrira xy. C'est dire, en particulier que x ⊕ y = xy + xy.

Associativité :   

Comparons (x ⊕ y) ⊕ z = x ⊕ (y ⊕ z). D'une part, par distributivité et par application des lois de Morgan :

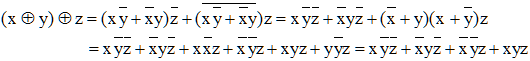
D'une part :

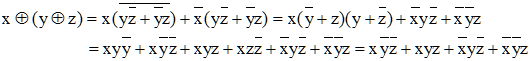
L'associativité est vérifiée.

Distributivité de la loi * sur la nouvelle addition :   

Il nous faut prouver que pour tous x, y et z de E, x*(y ⊕ z) = x*y ⊕ x*z. La loi * étant commutative, on peut se restreindre à prouver cette distributivité "à droite"). En écriture simplifiée, nous avons :

D'une part :

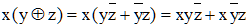
D'autre part, en appliquant les lois de Morgan :

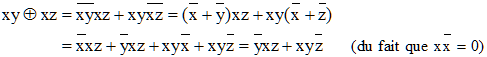
La distributivité est vérifiée.

En conclusion, (E,⊕,*) est un anneau commutatif (et unitaire puisque 1 est neutre pour *)

 ➔    Une application de ce résultat est donnée en tant qu'exercice à cet endroit.