
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

» cas d'un plan bitangent (cercles de Villarceau) | tore : aire & volume |

Le tore est une surface de l'espace engendrée par la rotation d'un cercle (c) autour d'un axe (d) situé dans son plan et ne le coupant pas. Une représentation simple et concrète en est une chambre à air de vélo ou une bouée. Selon Proclus, l'étude des sections d'un tore par un plan remonte au mathématicien grec Persée (Perseus, vers -250).
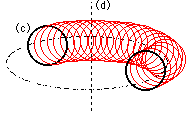
Rappelons que les sections d'un cône (sections coniques) et d'un plan furent étudiées par Ménechme et Apollonius. Les sections planes, d'un tore, sections spiriques (on coupe les spires du tore), sont moins connues. Elles font l'objet de cette page :
Plaçons-nous dans un repère orthonormal (O,x,y,z). L'axe des y étant choisi "vertical" eu égard aux considérations d'intersections planes à venir ci-après. Le centre A du cercle générateur est à la distance a de l'origine et son rayon est r. M est un point quelconque du tore généré dont l'axe sera (Oy).
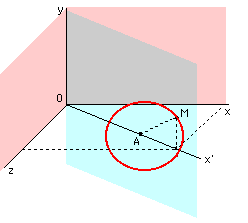
En notant X l'abscisse de M sur l'axe pivotant (Ox'), on a à chaque "instant" : X2 = x2 + z2. D'autre part M décrit, dans le plan (yOx') le cercle de centre A(a,0). Son équation est alors :
On remplace X par la racine carrée de x2 + z2. On développe, on isole le radical restant et on élève au carré. L'équation du tore est alors :
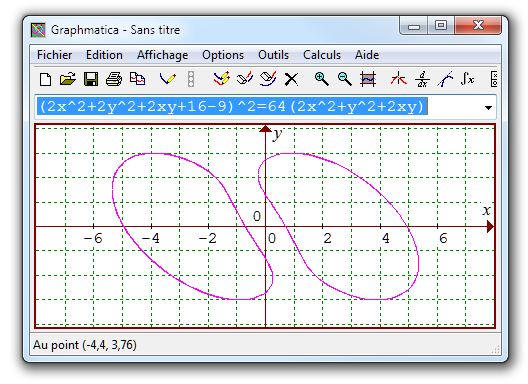
Nous allons couper le tore par un plan "vertical" (v) parallèle au plan (yOx), donc à l'axe du tore, dont l'équation sera alors de la forme z = d, constante positive mesurant la distance de (v) à l'origine. L'équation de l'intersection est obtenue en remplaçant z par d dans l'équation ci-dessus :
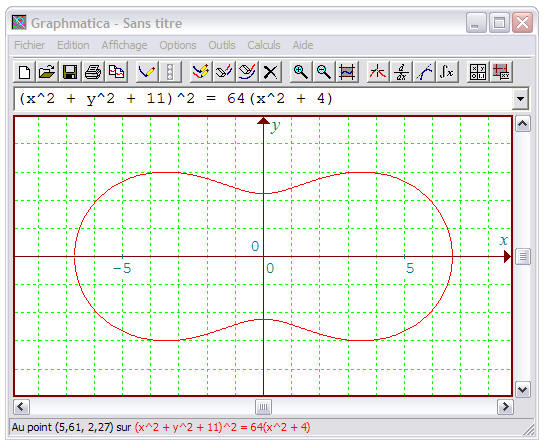
Tracé par Graphmatica, d =2, a
=4, r = 3
Les intersections sont simulées ci-dessous sur une chambre à air ayant durement souffert... :

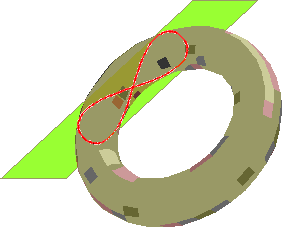
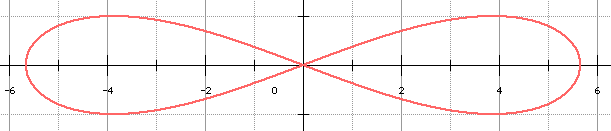
Lorsque a =
2r, on obtient la célèbre
lemniscate
de Bernoulli, cas
particulier d'ovale
de Cassini

➔ Les sections d'un tore par un plan parallèle à son axe seraient-elles des ovales de Cassini ? Non, sauf pour le cas d = r. Posons pour simplifier b2 = d2 + a2 - r2 (loisible puisque a > r). L'équation générale des courbes d'intersection est alors :
Nous savons que l'équation générale des ovales de Cassini est :
Il suffit de développer et d'identifier les deux équations pour obtenir m = b = a, puis d = r et k2 = 2ar :
Cette équation montre qu'un choix convenable de d conduit au fait que :
Nous voulons obtenir l'ovale de Cassini ci-dessous correspondant à : a = 2 et k = 5/2. Il suffit de choisir d = r = 25/16.
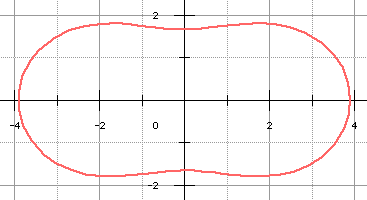
Nous voulons obtenir l'ovale de Cassini ci-dessous correspondant à : a = 3 et k = 2. Il suffit de choisir d = r = 2/3.

Nous voulons obtenir l'ovale de Cassini ci-dessous correspondant à : a = 3 et k = 2,97. Il suffit de choisir d = r = 1,47015.
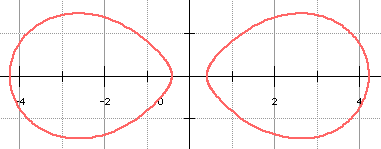
Si a = 2r, alors k2 = 4r2, donc k = 2r = a. On a aussi d = a - r. On retrouve la lemniscate de Bernoulli, cas particulier d'ovale de Cassini (k = a).
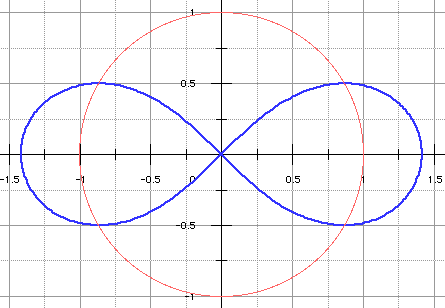
➔ On peut bien sûr chercher à intersecter le tore avec un plan quelconque. L'équation d'un tel plan est de la forme ax + by + cz + d = 0. Si c est non nul, on exprimera z en fonction de x et y : z = φ(x,y), et on reportera dans l'équation du tore :
Par exemple : x + y + z = 0 est l'équation d'un plan passant par O, dont on extrait z = - x - y :
» Guldin Villarceau et ses cercles : »