ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Un joli résultat (géométrie du triangle, triangles semblables)       niveau 3è/2nde

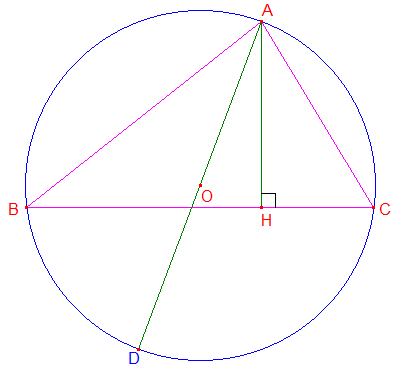
On considère un triangle ABC dont on a tracé la hauteur [AH], H intérieur à [BC]. On trace son cercle circonscrit et le diamètre [AD] passant par A.

1°/ Faire la figure
2°/ On demande prouver le résultat suivant :

AB × AC = AD × AH

Indication : on pourra tracer le segment [CD]

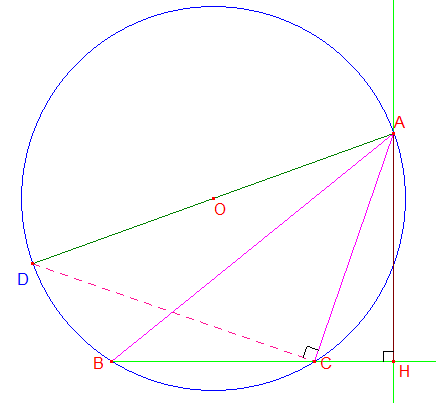
3°/ On suppose désormais que l'angle ^ACB du triangle ABC est obtus. Le résultat précédent est-il encore vérifié ?

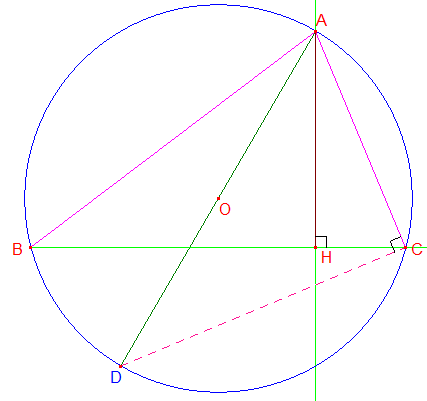
2°/ Le triangle AHB est rectangle en H. Il en est de même du triangle ACD rectangle en C car [AD] est un diamètre. L'angle inscrit ^ABC intercepte l'arc AC; il en est de même de l'angle inscrit ^ADC. Par suite, les triangles AHB et ACD sont semblables. En faisant correspondre correctement les angles de même mesure, on obtient AH/AC = AB/AD; autrement dit : AB × AC = AD × AH.

3°/ Là encore, les triangles AHB et ACD sont rectangles respectivement en H et C. Les angles inscrits ^ABC et ^ADC interceptent le même arc AC. Les triangles AHB et ACD sont donc semblables et on a comme précédemment : AB × AC = AD × AH.