
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
|
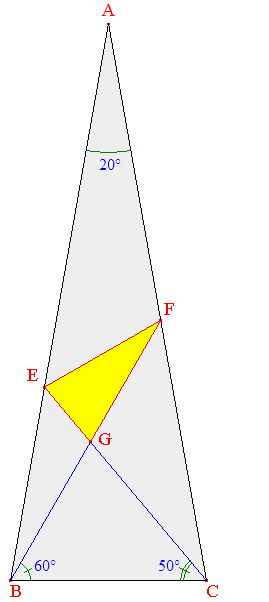 |
On considère un triangle isocèle ABC de sommet principal A.
On demande de calculer les mesures des angles du triangle EFG. Bon courage...
➔ Source de ce "petit" exo... : Redécouvrons la géométrie par H.S.M. Coxeter et S.L. Greitzer, Ed. Dunod 1971, ou encore : Géométrie classique et mathématiques modernes par Brigitte Sénéchal, Ed. Hermann, Paris - 1979. |
| Solution : |
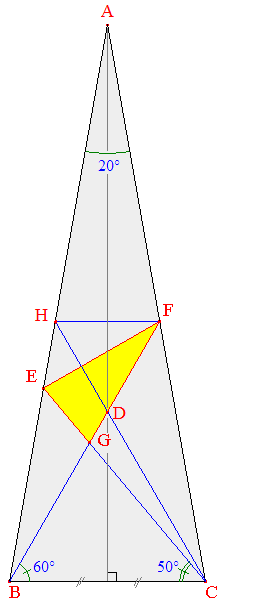 Un
triangle isocèle admet un axe de symétrie. La symétrie est ici cassée.
Rétablissons-la :
Un
triangle isocèle admet un axe de symétrie. La symétrie est ici cassée.
Rétablissons-la :
Pour ce faire, traçons l'axe de symétrie du triangle ABC, médiatrice de [BC].
Ainsi BC = BD et BE = BC, donc BE = BD.
On en déduit les égalités suivantes :
Par conséquent : EH = ED.
Mais HFD est équilatéral : donc FH = FD.
C'est dire que (EF) est la médiatrice de [HD].
Il suit que ^EFD = EFG = 30°.
^EGF = 180° - 60° - 50° = 70° et par suite ^FEG = 80°.
Les angles du triangle EFG mesurent 70°, 80° et 30°.
➔ Pas vraiment évident, voire infaisable, si nous n'avions pas pensé à rétablir la symétrie...