ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Le triangle égyptien #2    niveau 4è à 2nde                  » Un autre triangle égyptien | Triangles d'or | Voûte égyptienne

Outre le le triangle rectangle de côtés 3, 4, 5 et le triangle équilatéral, les égyptiens faisaient usage, selon Hérodote, d'un triangle isocèle dont la hauteur JS est établie en tant que nombre réalisant la section dorée de sa base AB :

Si AB = a et JS = h, alors h/a = 1/Φ = (√5 - 1)/2

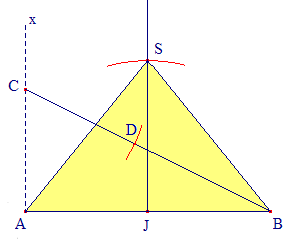
Construction de S :     

• La base est [AB] de centre J;
• Placer sur la perpendiculaire [Ax) le point C tel que AC = AJ.
• Tracer [BC];          
• Le cercle de centre C passant par A coupe [CB] en D;
• La section dorée est obtenue par D : BD/BA = 1/Φ;
• Reporter BD en JS sur la médiatrice de [AB].

On retrouve en fait ici, la construction de la section dorée selon Euclide. En posant AB = a, un calcul élémentaire, niveau 4ème, utilisant le théorème de Pythagore, montre que BD = a√5/2 - a/2 = a(√5 - 1)/2, inverse du célèbre nombre d'or.