
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

 |
» déplacements & antidéplacements |
On considère, dans le plan, la figure ci-dessous :
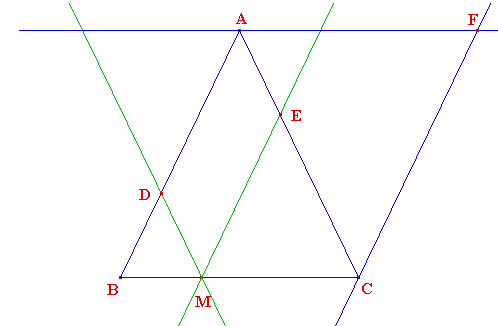
➔ Si votre navigateur le permet, voici la même figure générée par Cabri Géomètre dans sa version CabriJava pour Internet :

1. Prouver que AD = EC.
2. Soit f une isométrie transformant A en C, D en E. Prouver que f(B) =A.
3. On suppose de plus que f transforme C en F et on rappelle qu'une application affine est entièrement déterminée par l'image d'un repère affine du plan (donnée d'un triplet de points non alignés).
Soit d la droite des milieux parallèle à (BC) dans le triangle ABC. Montrer que f = T o Sd où T est la translation de vecteur ½BC.
➔ On dit que f est une symétrie glissée.
3. Vérifier que f = Sd o T = T o Sd : décomposition canonique de f.
| Solution : |
1. Bonne petite question niveau 5ème; trivial au niveau TerS/SUP...
2.
Posons a = DB, b = DA et B' = f(B). Le point D
est le barycentre de (A,a) et (B,b), on a donc la relation
a.DA + b.DB =
0.
La transformation f étant affine, elle conserve le barycentre, d'où :
a.EC + b.EB' =
0.
Or E est le barycentre de (A,EC) et (C,AE) et puisque AE = BD et DA = EC, on a
aussi :
a.EC + b.EA=
0. C'est dire que B' = A (unicité du
barycentre).

Si votre navigateur accepte les applets
Java
(»
extension CheerpJ![]() )
:
)
:
Vous
pouvez déplacer les sommets A, B et C du triangle ainsi que le point M
3.
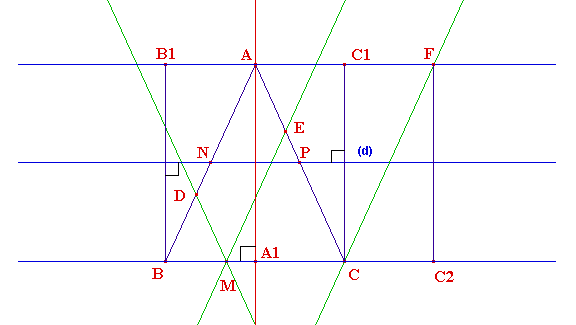
Traçons (d) = (NP) et la médiatrice de [BC];
elle coupe [BC] en son milieu A1. (AF) étant
parallèle à (BC), avec les notations ci-contre, B1ABA1
et AC1CA1
sont des rectangles isométriques et on a les égalités vectorielles ½BC =
B1A =
A1C.
C'est dire que :
T o Sd(A) = T(A1) = C et T o Sd(B) = T(B1) = A
D'autre part, dans le parallélogramme ABCF les triangles isocèles ABC et CFA s'échangent dans la symétrie de centre P, milieu de [AC]. D'où l'égalité vectorielle : C1F = ½BC et on a donc :
T o Sd(C) = T(C1) = F
➔ T o Sd coïncide donc avec F sur trois points non alignés : par conséquent f = T o Sd.
4.
Sd oT(A) = Sd
(C1)
= C;
Sd
oT(B) = Sd
(A1)
= A.
Notons C2 = T(C); CC1FC2
est un rectangle et
Sd
oT(C) = Sd
(C2)
= F. On peut donc conclure :
f = T o Sd = Sd oT