ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 
Suites de fonctions & convergence uniforme
niveau Sup |
1. On considère la suite de fonctions définie sur [0,1] par :
fn(x) = x(1 - xn)
a/ Montrer que la suite (fn) converge simplement sur l'intervalle [0,1].
b/ Étudier le sens de variations des fonctions fn sur [0,1]. Vérifier que fn admet un maximum absolu en un point xo que l'on précisera. Quelle est la limite pour n infini de xo et de ce maximum ?
c/ Montrer que la suite (fn) converge uniformément vers u sur tout intervalle [0,α], 0 < α < 1.
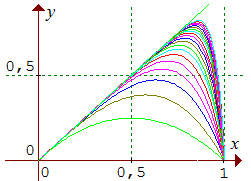
2. On considère la suite de fonctions définie sur R par :
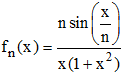
Montrer que la suite (fn) converge uniformément vers vers f : x → 1/(1 + x2)
