ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Résistances - loi des nœuds          » résistor et loi des mailles

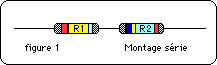
Dans un montage en série (figure 1) de deux résistances R₁ et R₂, notons :

• V la tension aux extrémités du circuit;
• V₁ la tension aux bornes de R₁;
• V₂ la tension aux bornes de R₂;
• i l'intensité qui le traverse (elle est la même en tout point du circuit puisqu'il n'y a pas de dérivation).

On a :

Ainsi la résistance équivalente est R = R₁ + R₂.

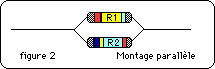
Plus subtil est le montage en parallèle (figure 2). En notant I₁ et I₂ les intensités traversant R₁ et R₂, on a i = I₁ + I₂ , la loi des nœuds conduit ici à :

∗∗∗

1. Montrer, par combinaison des proportions qui résultent des égalités ci-dessus que la résistance équivalente R vérifie :

2. On a mesuré au moyen d'un ohmmètre la résistance des circuits dans les deux cas de figure. Dans le premier cas (montage série), on a trouvé 1250 Ω et dans le second (montage parallèle) 288 Ω.

L'ohmmètre est maintenant cassé et les couleurs sur les résistances ne sont pas les bonnes...

Quelles sont les valeurs des résistances R₁ et R₂ ?

Cet exercice est une application de la recherche de deux nombres connaissant leur somme S et leur produit P. Ils sont solutions de l'équation :

On est conduit à l'équation du second degré :

On a √Δ = 350, d'où :

 ➔  le problème étant "symétrique" en R₁ et R₂, on ne peut savoir dans un tel cas laquelle des deux résistances vaut 450 Ω ou 800 Ω. En l'absence de l'ohmmètre, l'usage d'un ampèremètre permettra de les départager : en effet, la résistance la plus forte va s'opposer au passage du courant. Donc si I₁ < I₂, on aura R₁ = 800 Ω, sinon R₁ = 450 Ω.