ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Quadrature du rectangle     TD seconde         »  c'est quoi une quadrature ?             »   Quadrature du triangle , du pentagone

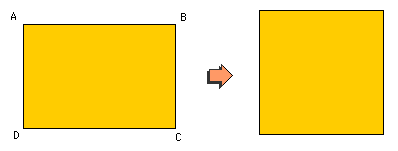
On considère un rectangle quelconque ABCD. Construire, au sens d'Euclide : règle (non graduée) et compas, un carré de même aire que le rectangle donné.

Solution proposée :    

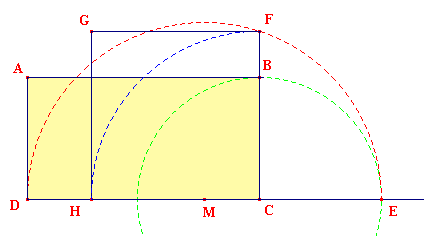
Voici le programme de construction. Le lecteur justifiera que le carré HGFC obtenu est bien de même aire que le rectangle ABCD initial. On suppose ici AB > CB.

1. Le cercle de centre C, de rayon CB, coupe (DC) en deux points : on appelle E le point extérieur au côté [DC].
    
2. On note M le milieu de [DE] et (c) le demi-cercle de rayon ME dans le demi-plan contenant B.
    
3. Soit F l'intersection de (c) avec la demi-droite [CB).
    
4. Le cercle de centre C de rayon CF coupe [DC] en H.
    
5. Le quadrilatère HCFG où G est le 4ème sommet du rectangle construit sur H, C et F est un carré de même aire que le rectangle ABCD.