ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 Pythagore,
Thalès, algèbre & trigonométrie contrôle des acquis
niveau 4è/3è |
1.
Développer et réduire (x
+ 2)2.
i
en
4è, on écrira que (x
+ 2)2 = (x
+ 2) × (x
+ 2) et on développera en utilisant la
distributivité de la multiplication sur
l'addition.
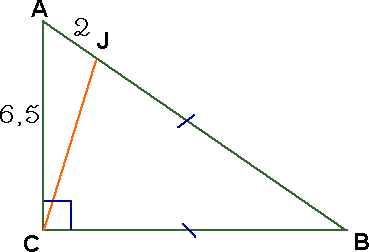
2. On pose CB = x. En utilisant la propriété de Pythagore dans le triangle ABC, calculer la valeur exacte de x puis donner la valeur arrondie au mm (le plus proche, comme ce doit toujours être le cas d'un arrondi), valeur que l'on utilisera dans toute la suite.
3. Montrer que la mesure arrondie au degré le plus proche, de l'angle ^CBA est 34°, valeur que l'on utilisera dans toute la suite.
4. En utilisant une propriété de la hauteur principale d'un triangle isocèle, calculer CJ en arrondissant le résultat trouvé au mm le plus proche.
5. Calculer la hauteur issue de J dans le triangle CJB en arrondissant le résultat trouvé au mm le plus proche en utilisant deux méthodes :
| Solution : |
1. (x + 2)2 = x2 + 4x + 4
2. Le triangle ABC est rectangle en C, son hypoténuse est AB; j'applique la propriété de Pythagore qui s'écrit ici :
Or, AB = BJ + JA = x + 2 , CA = 6,5 et CB = x, donc :
soit, avec usage de 1° et après réduction : 4x = 38,25, ce qui fournit x = 9,5625 (valeur exacte) et x = CB = 9,6 cm (arrondi au mm).
3. Dans le triangle ABC rectangle en C, on peut utiliser la trigonométrie :
cos ^CBA = BC/BA = 9,6/11,6.
La calculatrice fournit :
soit ^CBA = 34° en arrondissant au degré près.
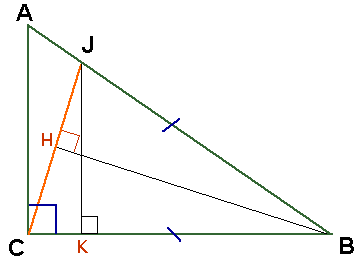
4. Dans un triangle isocèle, la hauteur issue du sommet principal est aussi la médiatrice de la base et la bissectrice de l'angle principal : ici, cette hauteur coupe perpendiculairement [CJ] en son milieu H.
On peut appliquer la trigonométrie dans le triangle BHJ, rectangle en H, avec ^JBH = 17° et ^HJB = 90° - 17° = 73° :
La calculatrice fournit JH = 2,806... cm, c'est dire que CJ = 5,612... cm, soit :