Point de Miquel #1

ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Point de Miquel #1 » #2 (cas plus général et cercle de Miquel)

Tracer un triangle ABC;
Placer un point A' sur ]BC[, un point B' sur ]AC[, un point C' sur ]AB[;
Tracer le cercle passant par A, B' et C';
Tracer le cercle passant par B, C' et A';
Tracer le cercle passant par C, A' et B'.

Ces trois cercles sont sécants en un point M. C'est un point de Miquel du triangle.

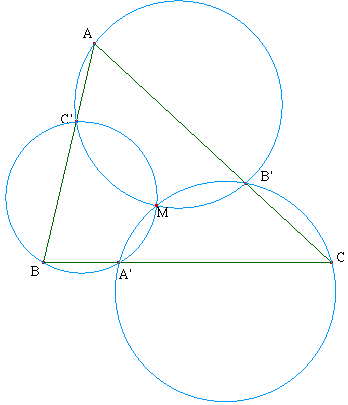
Si vous séchez après avoir bien cherché : ››››

Solution :

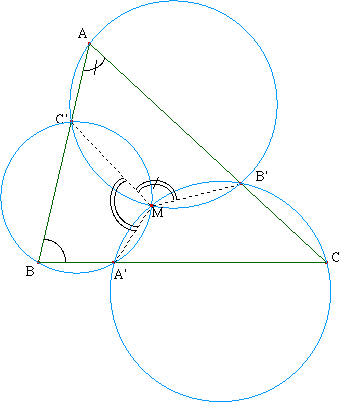
Considérons les cercles (AC'B') et (BC'A') se coupant en M. Les quadrilatères AC'MB' et BA'MC' étant inscriptibles, on a :

^A'MC' = 180° - ^B et ^B'MC' = 180° - ^A

Par suite :

^A'MB' = 360° - (180° - ^B) - (180° - ^A) = ^A + ^B = 180° - ^C

Par conséquent, les quatre points A', M, B' et C sont cocycliques : c'est dire que le cercle (CA'B') passe par M.

➔ On peut raisonner au moyen des angles orientés de droites (ou de vecteurs) pour une preuve moins élémentaire mais le point M se situant en l'intérieur du triangle ABC, on peut éviter de faire compliqué.

» Complément : que se passe-t-il si B', par exemple, est choisi en A (ou en C) ?

Cas plus général, A' sur [BC) non situé dans [BC] : ››››