
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
» proba #2 |
Voici une
roue de la fortune. L'heureux joueur sélectionné lance la roue et la somme
gagnée est celle qui correspond à la couleur marquée par l'onglet supérieur
 lorsque la roue s'arrête.
lorsque la roue s'arrête.
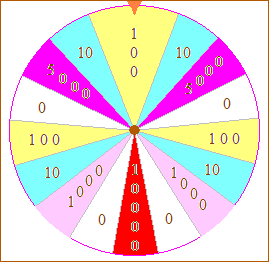
Toutes les tranches sont égales sauf une tranche de 100 € qui est double des autres.
Les sommes gagnées sont indiquées.
Si la roue s'arrête dans le blanc, on ne gagne rien mais mathématiquement c'est un gain : gain nul ! Le gain maximum est de 10 000 €.
On admet que toutes les positions d'arrêt de la roue ont la même probabilité de se réaliser et on appelle S la somme gagnée par un joueur (gain nul compris).
1°) Calculer, en justifiant brièvement, la probabilité de chaque valeur possible de S.
2°) Calculer, en justifiant brièvement, la probabilité des événements suivants :
a) Le joueur a gagné au moins 100 €.
b) Le joueur a gagné moins de 1000 €. c) Le joueur a gagné plus de 1000 €
| Réponses : |

Toutes les positions d'arrêt de la roue ayant la même probabilité de se réaliser (la roue n'est pas truquée...), la probabilité d'arrêt dans chaque tranche de même étendue est la même. On compte 16 tranches dont une tranche à 100 € qui, étant deux fois plus étendue, aura une probabilité de réalisation deux fois plus grande et comptera donc pour deux.
Tout se passe comme si nous avions 17 tranches d'égale probabilité. Les valeurs possibles de S sont 0, 10, 100, 1000, 5000 et 100000. Ainsi :
1°) P(S = 0) = P(S = 10) = 4/17 car il y a 4 tranches de gain 0 et 4 tranches de gain 10.
P(S = 100) = 2/17 +
1/17 + 1/17 = 4/17 car les cas favorables sont ici 1 tranche d'étendue double
de probabilité 2/17 et 2 tranches "normales"
de probabilité 1/17.
P(S = 1000) = P(S = 5000) = 2/17 car il y a 2 tranches de gain 1000.
P(S = 10 000) = 1/17 car il n'y a qu'une tranche de gain 10 000.
Résumé et vérification que la somme des probabilités est égale à 1 :
| Valeurs k de S | 0 | 10 | 100 | 1000 | 5000 | 10 000 | Vérif. |
| P(S = k) | 4/17 | 4/17 | 4/17 | 2/17 | 2/17 | 1/17 | 17/17 = 1 |
2°) a) Au moins 100 signifie 100 ou plus. En considérant l'événement contraire, on a :
P(S ≥ 100) = 1 - P(S < 100) = 1 - [P(S = 0) + P(S = 10)] = 1 - [4/17 + 4/17] = 9/17.
b) Un gain de moins de 1000 € se traduit par
S < 1000, donc par S = 0 ou bien S = 10 ou bien S = 100.
P(S = 10) = 4/17 et les
questions 2° et 3° permettent d'écrire :
P(S < 1000) = P(S = 0) + P(S = 10) + P(S = 100) = 4/17 + 4/17 + 4/17 = 12/17
c) Plus de 1000 € signifie S > 1000, soit ici S = 5000 ou S = 10000 :
P(S > 1000) = 2/17 + 1/17 = 3/17.
! "plus de 1000" (> 1000) n'est pas le contraire de "moins de 1000" (< 1000) car la négation de ">" est : "<" ou bien "=" ! On remarquera que :
P(S > 1000) + P(S < 1000) + P(S = 1000) = 3/17 + 12/17 + 2/17 = 17/17 = 1 : événement certain