ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Permutations circulaires      niveau Sup

Soit E = {a₁, a₂, ..., a_n} un ensemble non vide de n éléments distincts et k un entier naturel, k ≤ n. On considère l'application f_k de E dans E définie par :

Une telle application est une permutation circulaire de E.        

»  Exemple illustré de toutes les permutations de {a,b,c,d}

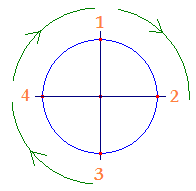
En termes concrets : c'est le principe des piles d'assiettes ! par exemple, une permutation circulaire de {1 , 2 , 3 , 4} est, en partant de 3 : {3 , 4 , 1 , 2 } : les assiettes 1 et 2 sont passées sous la 4 (la dernière), l'assiette 2 restant à la suite de la 1.

a/ Dans cette question seulement, on se place dans le cas n = 5 et k = 2. Montrer que :

f₂ o f₂ = f₄  , f₂ o f₂ o f₂ = f₁ , f₂ o f₂ o f₂ o f₂ o f₂ = id_E

b/ Montrer que f_k est une bijection de E sur E.

c/ Si k et k ' sont des entiers naturels inférieurs ou égaux à n, montrer que f_k o f_k' est une permutation circulaire de E.

d/ Plus généralement, on note :

• f_k⁽¹⁾ = f_k , f_k^(o) = id_E, (permutation identique).

• f_k^(p) = f_k^(p-1) o f_k , p-ème itéré de f_k pour la loi de composition des applications.

Montrer que f_k^(p) est une permutation circulaire de E.

e/ Préciser f_k^-1 et montrer que f_k^-1 est une permutation circulaire de E.

f/ Montrer, que muni de la loi de composition des applications, l'ensemble P des itérés de f_k est un groupe cyclique, sous-groupe du groupe symétrique de E, dont on donnera l'ordre.

Indications :  

a/ Faire un tableau d'images pour visualiser le processus.
c/ Soit r le reste de la division de k + k' par n...
e/ Considérer f_k o f_k^(n-1)...