ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Un petit problème de construction            niveau 4ème/3ème           » Construction au sens d'Euclide

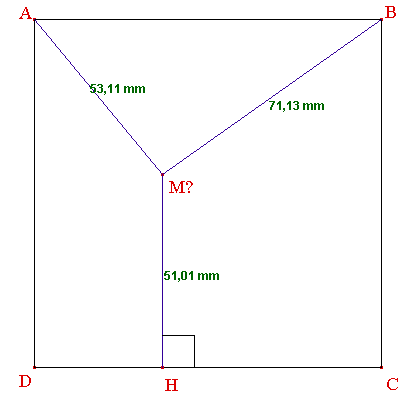
Et la même figure dans sa version CabriJava pour Internet :

Si votre navigateur accepte les applets Java (» extension CheerpJ) :
Tu peux déplacer le point M (et d'autres points) !

 

6è à 3è : Où placer le point M afin que MA = MB = MH ?

4è et 3è : On pose AB = a. Montrer que l'on a alors MH = 5a/8

Analyse :

• Puisque l'on doit avoir MA = MB, c'est que M est situé sur la médiatrice (d1) de [AB];
• Puisque l'on doit avoir MA = MH, c'est que M est situé sur la médiatrice (d2) de [AH];
• M est donc à l'intersection de ces deux médiatrices.

Construction :

• Au moyen de la règle et du compas, on trace la médiatrice (d1) de [AB];
• (d1) coupe [DC] en H, milieu de [DC];
• Au moyen de la règle et du compas, on trace la médiatrice (d2) de [AH];
• (d2) coupe (d1) au point M cherché.

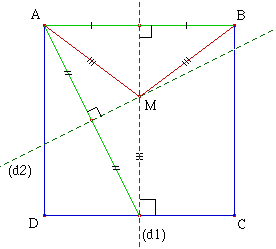
 ➔   On admet que (d1) et (d2) sont sécantes à l'intérieur du carré...

Synthèse :

• M est situé sur la médiatrice de [AB], donc MA = MB;
• M est situé sur la médiatrice de [AH], donc MA = MH;
• Si MA = MB et MA = MH, alors MB = MH.

On a donc bien MA = MH = MB.

Afin de calculer MH, utiliser le théorème de Pythagore dans un triangle rectangle d'hypoténuse AM dont un côté mesure a/2... En posant MA = x, vous serez amené à :

 ➔  En 4è, remarquer que :