ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Lunules d'Hippocrate        niveau 4ème       » Voir aussi : Aire d'une lunule

• 1 - Tracer un carré ABCD;

• 2 - Tracer les diagonales [AC] et [BD] de ce carré; elle se coupent en O;

• 3 - Tracer le cercle circonscrit au carré ABCD  (de centre O, il passe par les 4 sommets);

• 4 - Extérieurement au carré, tracer le demi-cercle de diamètre [AB];

• 5 - Faites de même pour les trois autres côtés.

• 6 - Colorier comme bon vous semble...

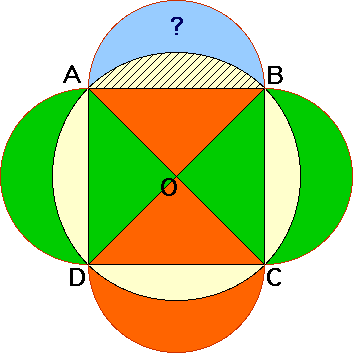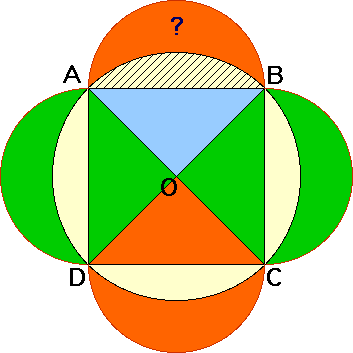
On se propose ici de prouver que l'aire de la lunule (portion de plan limitée par deux arcs de cercle de rayons distincts, ci-dessous marquée d'un point d'interrogation) est égale à l'aire du triangle OAB. Ou, ce qui revient au même, de prouver que :

l'aire du carré ABCD est égale à la somme des aires des quatre lunules.

Rappelons que la possibilité du calcul exact, sans usage du nombre π, de l'aire délimitée par deux cercles fut à l'origine des tentatives effrénées, durant des siècles, de la quadrature du cercle : construction, au sens euclidien, d'un carré de même aire qu'un cercle donné. On sait, depuis Wantzel (1837) qu'une telle construction est impossible.

Notons c le côté du carré. Par application du théorème de Pythagore dans le triangle rectangle isocèle AOB, la diagonale du carré a pour mesure c√2. Ainsi la demi-diagonale OA mesure c√2/2.

L'aire de la lunule supérieure (marquée d'un point d'interrogation) est égale à l'aire A₁ du demi-cercle de diamètre [AB] diminuée de l'aire A₂ de la calotte hachurée. L'aire d'un cercle de diamètre d est π × (d²/4). L'aire A₂ est la différence entre l'aire d'un quart de cercle de rayon c√2/2 et l'aire du triangle AOB :

• A₁ = ½ × π × (c²/4) = π × c²/8
• A₂ = π × (c√2/2)² /4 - c²/4 = π × c²/8 - c²/4

En conséquence : l'aire cherchée de notre lunule est c²/4, soit l'aire du triangle rectangle AOB. D'où le résultat :