ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 Le 8 du jardinier
TD niveau 1ère/Ter
(l'usage des angles exprimés en radians est plus aisé mais
facultatif ) |
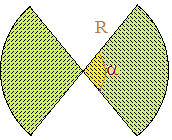
Un jardinier veut dessiner un parterre en forme de 8 qu'il bordera de petits ifs (arbustes verts à feuilles persistantes) espacés de 50 cm.
Le 8 sera constitué de deux secteurs circulaires identiques
opposés par leur centre commun (figure ci-dessus). Un des ifs sera
planté au centre. Notre jardinier a acheté 31 ifs.
1°) Pourquoi le choix d'un nombre impair d'ifs est-il
nécessaire ?
2°) Montrer que le demi périmètre p du parterre (périmètre d'un des deux secteurs) est 8 m.
3°) On note α l'ouverture des secteurs (exprimée en degrés ou en radians) et R leur rayon. Calculer le périmètre p puis l'aire A d'un secteur en fonction de R et α. Aide : » aire et périmètre d'un secteur circulaire.
4°)
Au moyen de 2° et 3°, montrer que
πRα
=360(4 - R). En déduire que l'aire A d'un secteur est égale à 4R - R2.
5°) Quelles devront être les dimensions des secteurs
(rayon et angle d'ouverture) afin
que l'aire du parterre soit maximale ? On pourra étudier la fonction f définie
par f(R) = 4R - R2
ou simplement remarquer que f(R) = 4 - (R - 2)2.
| Solution : |
1°) Quel que soit le nombre d'ifs de chaque secteur, sans tenir compte du centre qui appartient aux deux, on aura au total un nombre pair d'arbustes puisque la somme de deux nombres pairs ou de deux nombres impairs est paire. à ce nombre pair, on ajoute 1 pour l'if du centre. Ce qui fait bien, en tout, un nombre impair.
2°) Chaque secteur contient 15 ifs augmenté de celui du centre. Considérons un des secteurs. C'est un contour fermé contenant 16 ifs équidistants de 50 cm. Le demi-périmètre est donc 16 x 0,5 m, soit 8m.
Solution avec α exprimé en radians :
3°) Considérons le demi-parterre.
Son périmètre est 2R + 2πR × α/2π = 2R + Rα.
L'aire d'un secteur de rayon R, d'ouverture α est A = πR2 × α/2π = R2α/2.
4°) Selon 2°, le demi-périmètre est 8 m. On a donc 2R + Rα = 8. D'où Rα = 8 - 2R. L'aire d'un secteur est A = R2α/2. En remplaçant Rα par 8 - 2R, on en déduit que A = R(8 - 2R)/2, c'est à dire :
A = 4R - R2
5°) L'aire du parterre sera maximale lorsque l'aire d'un secteur le sera, c'est à dire lorsque 4R - R2 sera maximal. f(R) = 4R - R2 peut s'écrire 4 - (R - 2)2 : un carré étant toujours positif, on a - (R - 2)2 ≤ 0. La plus grande valeur de f est donc obtenue si R = 2. On a alors f(2) = 4 (l'aire d'un secteur est 4 m2) et Rα = 8 - 2R devient 2α = 4, ce qui fournit α = 2.
Réponses : R = 2 ; α =2 radians, Aire totale = 4 m2.
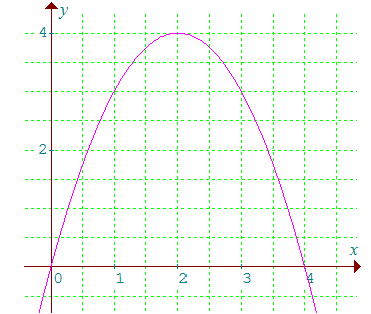
Représentation de f sur l'intervalle
[0,4], parabole de sommet S(2,4)
Solution avec α exprimé en degrés :
3°) Considérons le demi-parterre.
Son périmètre est 2R + 2πR × α°/360 = 2R + πRα°/180.
L'aire d'un secteur de rayon R, d'ouverture α° est A = πR2 × α°/360.
4°) Selon 2°, le demi-périmètre est 8 m. On a donc 2R + πRα°/180 = 8. D'où πRα° = 180(8 - 2R) = 360(4 - R).
L'aire d'un secteur est A = πR2α°/360. En remplaçant πRα° par la valeur calculée précédemment, on en déduit que l'aire est :
A = 360(4 - R) × R/360 = 4R - R2.
5°) L'aire du parterre sera maximale lorsque l'aire d'un secteur le sera, c'est à dire lorsque 4R - R2 sera maximal. f(R) = 4R - R2 peut s'écrire 4 - (R - 2)2 : un carré étant toujours positif, on a - (R - 2)2 ≤ 0. La plus grande valeur de f est donc obtenue si R = 2. On a alors f(2) = 4 (l'aire d'un secteur est 4 m2) et πRα = 360(4 - R) devient 2πα = 720, ce qui fournit α ≅ 115°.
Réponses : R = 2 ; α ≅ 115°, Aire totale = 4 m2.
Représentation de f sur l'intervalle
[0,4], parabole de sommet S(2,4)