
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
» π par quadrature (approchée) du cercle... (TP 5è/4è) | Aire d'un disque (TD 6è/3è) » Le cercle selon Archimède | Calculs de π dans ChronoMath | Les 10 000 premières décimales de π |

Voici une séance de travaux pratiques mathématiques où les élèves amenèrent chacun, à la demande du professeur, une boîte de conserves cylindrique en bon état (vide ou pleine, non cabossée), débarrassée de son étiquette et de diamètre suffisamment grand afin d'en faciliter une mesure relativement précise. Les apports des élèves furent divers (thon, cœurs de bambous, crème dessert, ...) : une diversité indispensable pour convaincre les élèves, en fin d'étude, que π ne dépend pas du diamètre du cercle !
Outils :
règle graduée (plastique transparent), adhésif (type
scotch), ciseaux, calculatrice
Manips (élève seul ou en binôme) :
1. Mesure avec soin, au mm près, le diamètre d de la boîte en plaçant sur son dessus un double décimètre que tu feras pivoter doucement en maintenant le 0 sur un bord jusqu'à obtenir la plus grande mesure, c'est à dire le diamètre.
!
Pense à
corriger cette mesure en tenant compte de
l'épaisseur de la soudure
qui augmente le diamètre réel de la boîte.

2. Procéde soigneusement à 2 autres mesures à partir de points de départ différents. Conserve la plus petite mesure (m) et la plus grande (m') et choisis pour d la moyenne arithmétique des deux. Compléte :
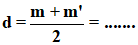
Si tes trois mesures sont identiques, compléte simplement :
d = .......
3. Enroule un ruban adhésif transparent ("scotch") autour de la boîte en prenant garde à ne pas aller de travers : rester bien "parallèle au bord" supérieur (ou inférieur) de la boîte. Évite d'appuyer "trop fort" contre la boîte.
!
Ne pas étirer pour ne pas fausser la mesure qui va
suivre.
Ayant fait un un peu plus qu'un tour complet, note avec un stylo à bille ou un feutre fin l'endroit précis de recouvrement avec le début de l'enroulement en évitant de coller trop fort l'adhésif sur lui-même. Couper ensuit ce dernier au delà de la marque.
4. Déroule maintenant doucement l'adhésif : cela devrait se faire sans difficultés. En cas de problème, refais la manip 3 en appuyant moins fort contre la boîte.
5. Mesure soigneusement la longueur L de la bande d'adhésif : comme pour le diamètre, procéde à trois mesures au mm près conduisant à :
L = .......
6. On va maintenant diviser L par d. Utilise ta calculatrice afin de calculer le quotient L/d à 0,01 près : on ne conserve que deux décimales. Un résultat comme 3,12375... sera arrondi à 3,12; un autre comme 3,13728... sera arrondi à 3,14.
7. Exposé des résultats :
 Chaque élève ou le représentant de son binôme
inscrit ses mesures et calculs dans le tableau préalablement préparé par le
professeur. Voici quelques résultats de mesures effectives :
Chaque élève ou le représentant de son binôme
inscrit ses mesures et calculs dans le tableau préalablement préparé par le
professeur. Voici quelques résultats de mesures effectives :
| d | 9,9 | 5,2 | 10 | 8,35 | 7,3 | 8,4 | 9,95 |
| L | 31,3 | 16,4 | 31,3 | 26,2 | 23 | 26,4 | 31,3 |
| L/d | 3,1616... | 3,1538... | 3,13 | 3,1377... | 3,1506... | 3,1428... | 3,1457... |
| L/d | 3,16 | 3,15 | 3,13 | 3,14 | 3,15 | 3,14 | 3,15 |
8. Conclusion : découverte du nombre π (prononcer "pi") :
La dernière ligne du tableau ci-dessus indique les valeurs approchées du quotient L/d. On admettra que les différences observées de ce quotient sont dues à l'imprécision des mesures ou des défauts des boîtes utilisées. Complète alors :
Le quotient de la ............. du périmètre
d'un ........... par son ............... est le .....ê.... pour tous
les ............
Ce quotient est un .............. appelé π.
(c'est le p grec et la première lettre du mot grec
perifereia = périphérie,
circonférence)
Autrement dit, en notant R le rayon du cercle :
Le périmètre du cercle est égal au produit de son diamètre par le nombre π :
L = π × d = 2π × R
➔ Ce résultat exprime également que :
Le périmètre d'un cercle proportionnel à son diamètre
Depuis l'époque d'Archimède de Syracuse (250 ans avant J.-C.), les mathématiciens ont calculé des valeurs de plus en plus précises de π. Ce nombre possède une infinité de décimales ! Et ce n'est pas une fraction : il n'est pas le résultat de la division de deux nombres entiers :
π ≃ 3,141592653589793238462643383279...
On peut retenir qu'une bonne approximation de π à quatre décimales (au dix-millième près) est 3,1416. A l'école et au collège, avant l'usage des calculatrices, on utilisait souvent 3,14 ainsi que l'approximation fractionnaire 22/7 ≃ 3,1428.
♦ Le diamètre d'une roue de vélo, pneu compris, est 69,2 cm. De combien de mètres avance-t-on en 1 tour de roue (donner la réponse au cm près) ? Rép. : la calculatrice fournit π × d = 217, 3982116 cm, soit 2,17 m. En utilisant π = 3,14, la réponse est la même. Au mm près, la réponse est 2,174 avec la précision de la calculatrice et 2,173 au moyen de π = 3,14.
Remarques :
r1/ Comme le montre les cas d = 9,9 et d = 10 ci-dessus, le quotient L/d est très sensible : un écart d'un mm sur le diamètre génère trois centièmes d'écart sur le quotient. La mesure d = 9,95 (moyenne d'une mesure m = 9,9 et m' = 10) et L/d ≃ 3,15 est un résultat très acceptable eu égard à cette méthode très rustique du calcul de π, montrant tout l'intérêt de tenir compte de l'incontournable imprécision des mesures.
r2/ Pour cet échantillon, la moyenne des quotients L/d est 3,1457..., soit 3,15 en arrondissant au centième. En refusant les cas montrant manifestement des erreurs de mesure, la classe a obtenu un encadrement de π entre 3,12 et 3,16 et une moyenne (sur 21 mesures acceptées) également de l'ordre de 3,15.