ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Intersection de plans  #3       niveau 2nde             » #1 , #2 , #4      » voir aussi...

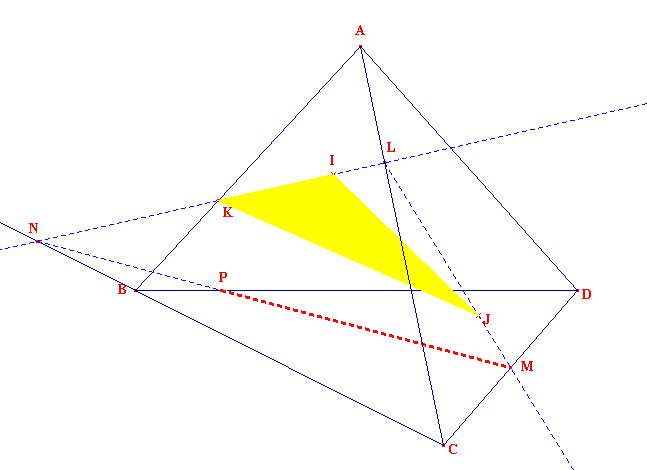
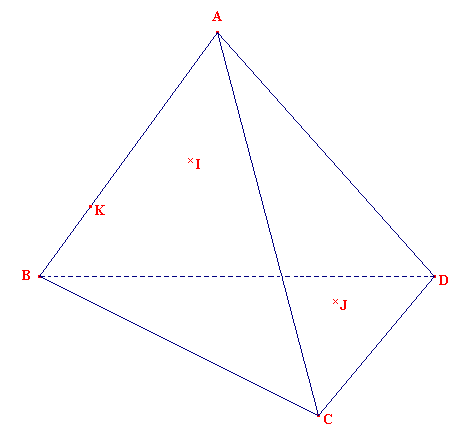
Voici un tétraèdre ABCD. I est situé dans la face ABC, J est situé dans la face ACD, K est un point de l'arête [AB]. On demande de construire l'intersection (section) du plan (IJK) avec la base BCD.

• La droite (IK) coupe [AC] en L. L 'est un point de (IJK).

• La demi-droite [LJ) coupe [CD] en M. M est un point de (IJK) puisque (LJ) est incluse dans (IJK). Et M est un point de la base BCD.

• La droite (IK) coupe le prolongement de [CB] en N : c'est un point de (IJK) et un point de la base BCD.

• (NM) est une droite de (IJK) et de (BCD). Traçons [NM] coupant [BD] en P.

L'intersection cherchée est le segment [PN].