ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 
Cinq petits exos de gymnastique bilinéaire
niveau Sup |
» Les cinq exercices sont indépendants. On se référera tout d'abord aux définitions en cliquant sur la clé. Une fois n'est pas coutume, les solutions ne sont pas données. Mais si vous séchez ou si vous constatez une erreur d'énoncé, vous pouvez me contacter.
1. Montrer que :
i/ Toute application bilinéaire alternée est antisymétrique
ii/ A
l'exception du cas où le corps de scalaires K est de
caractéristique
2, toute application bilinéaire antisymétrique est
alternée.
Indication : pour tout x non nul,
x + x = 2x est non nul puisque K n'est pas de caractéristique 2, et f(2x,x)
= -f(x,2x)...
iii/ Dans le corps fini K = Z/2Z = {0,1} des classes résiduelles modulo 2 considéré comme espace vectoriel sur lui-même, montrer que toute forme bilinéaire sur K, vérifie : f(x,y) = xy.f(1,1).
4i/ On pose
alors, afin que f ne soit pas nulle : f(1,1) =
1. Montrer que f est à la fois symétrique et
antisymétrique, mais non alternée.
2. On considère une application bilinéaire f de E x F vers G. Montrer que f(x,y) = 0G dès que l'un au moins des vecteurs x et y est nul (x = 0E ou x = 0F).
3. Montrer que l'application nulle θde E × F vers G, qui à tout (x,y) associe 0G, est à la fois linéaire et bilinéaire de E x F vers G (voir encadré vert ci-dessus).
4. E désigne un espace vectoriel de dimension 3 sur R. B = (i,j,k) est une base de E et f l'application de E x E vers E définie par :
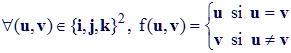
Montrer que :
a/ f est bilinéaire, non symétrique.
b/ Si V(x,y,z) et W(x',y',z') relativement à B, alors :
f(V,W) = (xx' + yx' + zx').i + (xy' + yy' + zy').j + (xz' + yz' + zz').k
5. On considère une forme bilinéaire et symétrique f sur un plan vectoriel réel P (espace vectoriel de dimension 2 sur R) rapporté à la base (i,j).
i/ Montrer que v = x.i + y.j et w = x'.i + y'.j , alors :
f(v,w) =xx'.f(i,i) + (xy' + x'y).f(j,i) + yy'.f(j,j)
ii/ On dit qu'un vecteur u est unitaire relativement à f, si f(u,u) = 1 et que deux vecteurs v et w de P sont orthogonaux pour exprimer que f(v,w) = 0.
En supposant alors que la base (i,j) est unitaire : f(i,i) = 1 et f(j,j) = 1 et orthogonale : f(i,j) = f(j,i) = 0, montrer que v = a.i + b.j et w sont orthogonaux si et seulement si w = kb.i - ka.j où k est un réel quelconque.