ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

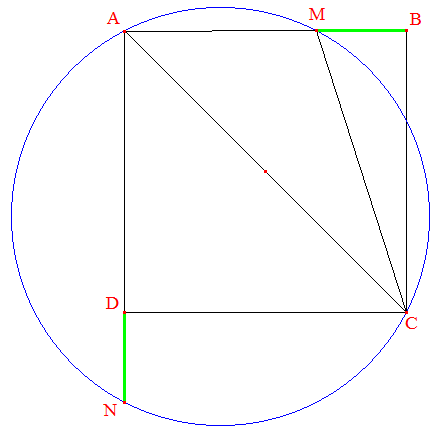
• On considère un carré ABCD;

• M est un point de [AB];

• (c) est le cercle circonscrit au triangle AMC;

• [AD) coupe (c) en N.

On demande de prouver que MB = DN.

Indications :
prouve que MCN est rectangle et isocèle en C et considérer ensuite la rotation qui transforme B en D...

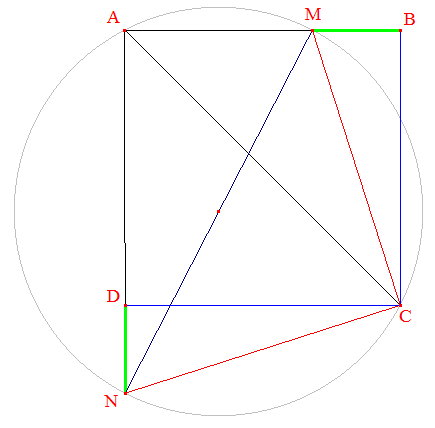
•  ABCD étant un carré, ^MAN est droit; [MN] est donc un diamètre et C étant sur le cercle, ^MCN est également droit.

•  [AC] étant une diagonale du carré, ^MAC = 45°;

•   Mais ^MNC = ^MAC (angle inscrits interceptant le même arc. Par suite, le triangle MNC est rectangle isocèle.

Considérons maintenant la rotation r de centre C, d'angle 90° transformant B en D. Selon le résultat prouvé ci-dessus, elle transforme M en N; donc BM = DN.

Dans le bon vieux temps, on aurait pu conclure en utilisant les cas d'égalité des triangles rectangles :
MBC et NDC sont rectangles, ils ont l'hypoténuse égale (CM = CN) et un côté de l'angle droit égal (CB = CD).
ils sont donc "égaux" (isométriques), d'où BM = DN.