ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Suites adjacentes     extrait Bac S, Antilles-Guyane, juin 2005

Préliminaires :    

a) Prouver que pour tout entier naturel non nul n et pour tout élément x de [0,1], on a :

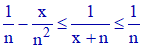
b) Calculer l'intégrale :

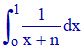
c) Déduire des résultats précédents que pour tout entier n non nul, on a :

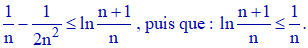
d) Comparer maintenant :

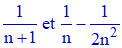
1°/ On note U la suite définie pour tout n non nul par :

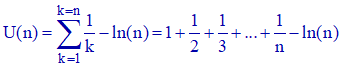
Prouver que la suite U est décroissante.

2°/ On note maintenant V la suite définie pour tout n non nul par :

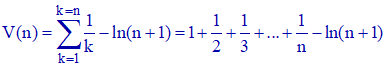
Prouver que la suite V est croissante.

3°/ Démontrer que U(n) et V(n) sont convergentes vers une limite commune α. On précisera le rang n assurant une valeur approchée de α à 10^-2 près.

Si vous séchez après avoir bien cherché : ››››

Préliminaires :    

a) Considérons la 1ère inégalité :

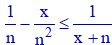
Elle équivaut à :

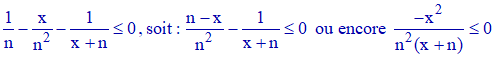
L'inégalité est donc vérifiée. Quant à la seconde inégalité, elle est clairement vérifiée puisque n est non nul et x dans [0,1].

b) L'intégrale proposée existe et est finie puisque l'intégrande 1/(x + n) est continue sur [0,1], n n'étant pas nul.

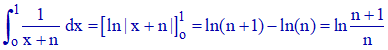
c) Intégrons sur [0,1] la double inégalité proposée en préliminaire a) :

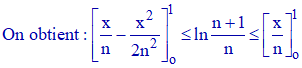
C'est à dire :

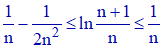
d) Considérons la différence :

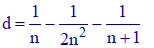
On réduit au même dénominateur :

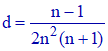
n étant non nul, on a d ≥ 0. C'est dire que :

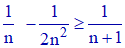
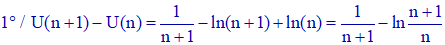
Selon d), nous avons :

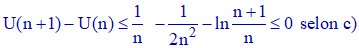
Ainsi, U(n+1) ≤ U(n) pour tout n de N* : la suite U est décroissante.

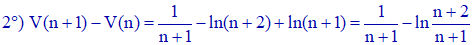
Selon les préliminaires c), pour tout n non nul, on a :

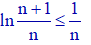
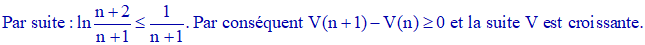
4°) On note que U(n) - V(n) = ln(1 + 1/n) ; donc U(n) - V(n) tend vers ln1 = 0. Les suites U et V, respectivement décroissante et croissante, sont donc adjacentes : elles convergent donc et ont la même limite. Pour tout n non nul, on a V(n) ≤ α ≤  U(n). La limite α sera approchée à 10^-2 près dès lors que ln(1 + 1/n) sera inférieur à 10^-2 :

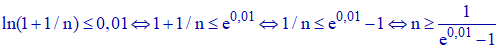
Ce qui fournit n ≥ 99,5 que l'on arrondit à n = 100.

 ➔   Ce petit programme JavaScript conduit à α ≈ 0,58220, soit 0,58 à 10^-2 près pour n = 100 :

<SCRIPT LANGUAGE=JavaScript>function go()
{
n=0
som=0
while (n<100)
 {
 n++
 som=som+1/n
 }
 L=Math.log(n)
 U=som-L
alert("n="+n+" somme = "+U)
}
</SCRIPT>

<CENTER>
<HR width="40%">
<INPUT TYPE=button NAME=Bouton VALUE="Lancer le programme" onclick="go()">
<HR width="40%">
</CENTER>