ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Deux échelles sont appliquées entre deux murs comme indiqué ci-dessous. La plus courte repose en A à 5 m de hauteur; la plus longue repose en C à 7 m. La distance entre les deux murs est de 3 m. A quelle hauteur les échelles se croisent-elles ?

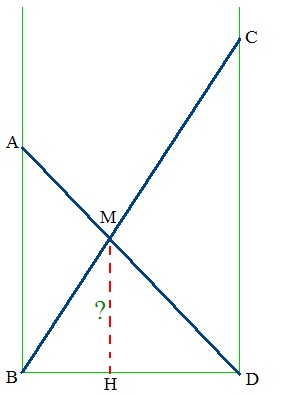
La figure ci-dessus n'est pas à l'échelle...

Indications pour une méthode 1 (propriété de Thalès) : 

• On note BH = a et MH = h.

• En justifiant du bon usage de la propriété de Thalès dans les triangles BDC et ADB, montrer que l'on a respectivement 3h  = 15 - 5a et 3h = 7a.

• En déduire a, puis h = MH.

Indications pour une méthode 2 (équations de droites) : 

• On se place dans le repère orthonormé d'origine B, l'axe des abscisses est orienté de B vers D, l'axe des y de B vers A.

• La distance cherchée est l'ordonnée du point M, intersection des droites (AD) et (BC).

Méthode 1 :

Selon le théorème de Thalès appliqué dans le triangle BCD coupé par la droite (MH) parallèle au côté [CD], on peut écrire :

BH/BD = MH/CD

soit :

ou encore :

3h = 7a

Selon le théorème de Thalès appliqué dans le triangle BAD coupé par la droite (MH) parallèle au côté [AB], on peut écrire :

DH/DB = MH/AB

soit :

ou encore :

3h = 15 - 5a

On en déduit :

7a = 15 - 5a

12a = 15

a = 1,25

puis :

3h = 7a = 8,75

soit :

h ≅ 2,92 m

Méthode 2 :

En prenant le mètre comme unité, nous avons :

• B(0;0)
• A(0;5)
• D(3;0)
• C(3;7)
• et on pose M(x;y)

- Une équation de la droite (BC) est y = 7x/3

- Une équation de (AD) est y = -5x/3 + 5

L'abscisse de M, intersection des droites (BC) et (AD) est fournie par l'équation 7x/3 = -5x/3 + 5.
Ce qui conduit à 4x = 5, donc à  x = 1,25, puis y = 7x/3 ≅ 2,92

Les échelles se croisent donc à 2, 92 m