ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Deux jetons !          probabilités conditionnelles       niveau Ter

» Cet exercice est extrait des énigmes mathématiques de Lewis Carroll :

Un sac contient un jeton dont on sait qu'il est jaune ou bleu. On ajoute dans le sac un jeton jaune identique au toucher à celui déjà présent. On secoue le tout, on tire un jeton et on constate alors qu'il est jaune.

Quelle est la probabilité que le jeton restant soit jaune ?

Soit J1 (resp. J2) la probabilité de tirer un jeton jaune au 1er (resp. au second) tirage. Notons également respectivement JJ, BB, JB les événements le sac contenait avant le 1er tirage deux jetons jaunes, deux jetons bleus, un jeton jaune et un jeton bleu (l'événement BB est impossible par hypothèse).

La probabilité cherchée est la probabilité de réalisation de J2 sachant J1 réalisé, c'est à dire la probabilité conditionnelle P(J2/J1), également notée P_J1(J2). On sait que :

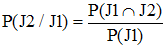
J1 a pu se réaliser dans deux situations initiales, à savoir, en termes ensemblistes : JJ ∪ JB. On peut alors écrire :

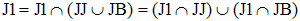
Donc P(J1) = P(J1/JJ)×P(JJ) + P(J1/JB)×P(JB)

• P(J1/JJ) = 1 : sachant les deux jetons jaunes, on tirera du jaune !

• P(JJ) = 1/2 : on a mis un jeton jaune dans un sac contenant un jaune ou un bleu.
  On a donc 1 chance sur 2 d'avoir un second jeton jaune.

• P(J1/JB) = 1/2 : s'il y a initialement un jaune et un bleu, on a une chance sur 2 de tirer un jaune.

• P((JB) = 1/2 : le jeton jaune est assuré. On a, là encore, 1 chance sur 2 que le jeton initial soit bleu.

Par conséquent, P(J1) = 3/4.

J1 ∩ J2 ne peut avoir lieu que s'il y avait 2 jetons jaunes. Inversement 2 jetons jaunes initialement implique la réalisation de J1 ∩ J2. C'est dire que P(J1 ∩ J2) = P(JJ) = 1/2.

En conclusion :     

La probabilité cherchée est 1/2 ÷ 3/4 = 2/3.