ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
Une application de la notion de fonction affine |
 Gabriel Daniel Fahrenheit
(physicien allemand, 16861736) donna son nom à la première échelle de
température (1709) qu'il mit en pratique au moyen d'un thermomètre
(du grec thermon = chaleur et metron = mesure) à
mercure. Son unité, le
degré
Fahrenheit (°F) est encore utilisée en Angleterre et en Amérique du nord.
Gabriel Daniel Fahrenheit
(physicien allemand, 16861736) donna son nom à la première échelle de
température (1709) qu'il mit en pratique au moyen d'un thermomètre
(du grec thermon = chaleur et metron = mesure) à
mercure. Son unité, le
degré
Fahrenheit (°F) est encore utilisée en Angleterre et en Amérique du nord.
L'échelle la plus répandue aujourd'hui est due (1742) à Anders Celsius (astronome et physicien suédois, 1701-1744); c'est une échelle centésimale : 0° Celsius (0°C) correspond aujourd'hui au point de congélation de l'eau, 100°C correspond au point d'ébullition (à l'origine, Celsius avait inversé ces valeurs).
Le mercure est un métal "liquide" dangereux, polluant et couteux. On utilise de nos jours des thermomètres à alcool. On le rencontre encore des les baromètres de Torricelli.
Il existe entre les degrés Fahrenheit et Celsius une correspondance affine : si F est la température en °F et C celle en °C, on a :
C = aF + b
1°/ Calculer les coefficients a et b sachant que :
0°C correspond à 32°F
100°C correspond à 212°F.
2°/ Écrire F en fonction de C.
Indications et solution :
1°/ Selon l'énoncé, C est une fonction affine de F, tout comme lorsque y = ax + b signifie que y est une fonction affine de x.
Les données permettent d'écrire que :
si F = 32, on a C = 0, c'est à dire : 32a + b = 0;
Si F = 212, on a C = 100, c'est à dire 212a + b = 100.
Ces deux équations constituent un système
linéaire très simple de deux équations à deux inconnues a et b.
On trouvera aisément que a = 5/9 et b = -160/9 :
![]()
2°/
![]()
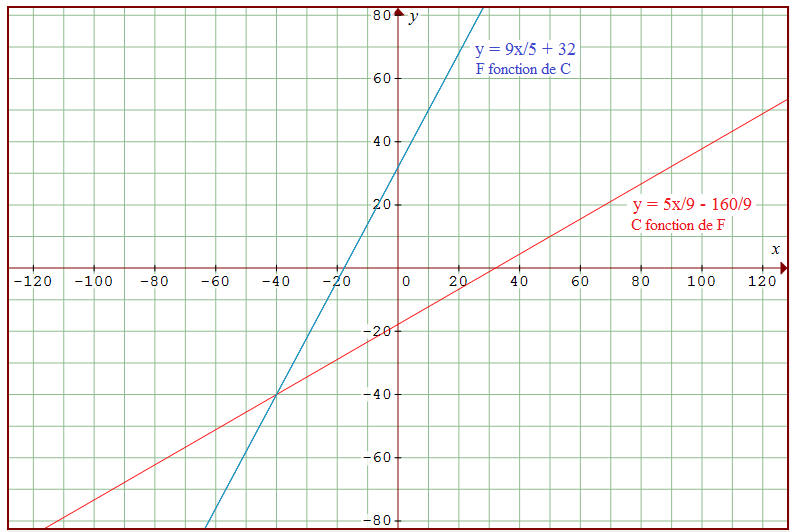
Prolongement :
On a représenté ci-dessous dans un même repère, les fonctions x →y = 9x/5 + 32 (x est alors la température en °C et y celle en °F) et x →y = 5x/9 - 160/9 (x est alors la température en °F et y celle en °C). On voit qu'il existe une température (sibérienne) telle que les thermomètres indiquent le même nombre en °C et °F.