ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 

Apprendre à construire, démontrer, rédiger : médiatrice & cercles     •••             niveau 6ème/4ème      » objectif

1°/  Rédige le programme de construction de cette figure et énonce la question.

2°/  Essaie de prouver ce que tu as certainement bien énoncé.

1°/

• On considère deux cercles de centres respectifs A et B de rayons distincts (différents).
• Ces cercles se coupent en E et F.
• Tracer la droite (EF)

Prouver que la droite (EF) est perpendiculaire au segment [AB].

 

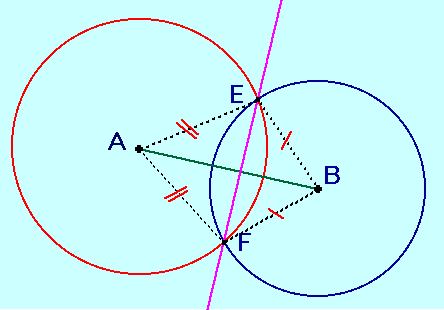
2°/

Preuve :

Traçons les segments [AE], [AF], [BE] et [BF]. On a :

• d'une part : A... = A... en tant que rayons du cercle de centre A.
• d'autre part : ...... = ...... en tant que rayons du cercle de centre B

On connaît les définitions ou propriétés suivantes :

• La médiatrice d'un segment est la droite ............................... à ce segment en son ................;
• Tout point situé à égale distance des extrémités d'un segment est situé sur ........................ de ce segment;
• Une droite est déterminée par deux de ses points.

En conséquence :

• A est situé sur la médiatrice de ......... puisque AE = AF
• B est situé sur la médiatrice de ......... puisque BE = BF

En conclusion :

La droite (AB) est la .................... de [.......] ; elle est donc perpendiculaire à la droite (EF) et on peut aussi dire que la droite (EF) est perpendiculaire au segment [AB].

 ➔   Variante : si les cercles sont supposés avoir le même rayon, le quadrilatère AEBF est un losange et on peut montrer la perpendicularité cherchée en utilisant la propriété selon laquelle les diagonales d'un losange sont perpendiculaires.