ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Construire un cercle passant par 2 points et tangent à une droite     Ce problème correspond au problème n°2 d'Apollonius, dit PPD, résolu par Viète en l'an 1600

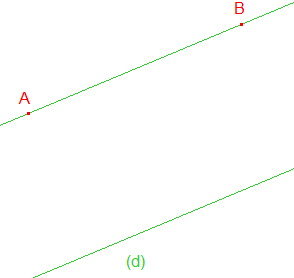
Dans un plan, on se donne deux points A et B et une droite (d) ne passant pas par ces points.

Construire un cercle tangent à (d) et passant par A et B

On distinguera deux cas : 

a) (AB) parallèle à (d)                                    b) (AB) non parallèle à (d) coupant (d) en E.

                    

 i  La résolution de ce problème de construction fait appel à la puissance d'un point par rapport à un cercle.

Si vous séchez après avoir bien cherché : ››››

---

© Serge Mehl - www.chronomath.com

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Rappel : la tangente en un point C d'un cercle de centre O est la droite perpendiculaire au rayon [OC].

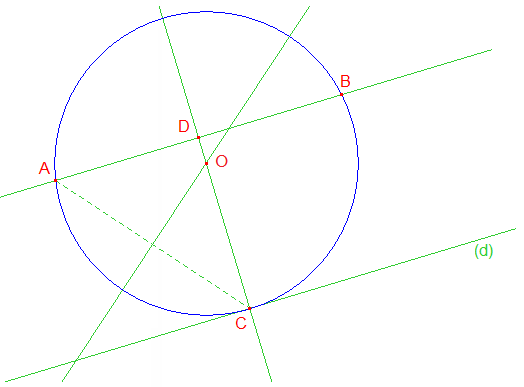
a) Si (AB) est parallèle à (d), traçons la médiatrice de [AB] : perpendiculaire à (AB) passant par le milieu D de [AB]; elle coupe (d) en C. Le centre O du cercle cherché est équidistant de A et B et situé sur cette médiatrice. On a (OC) perpendiculaire à (d). C'est dire que C est le point de contact cherché avec le cercle solution qui est donc tout simplement le cercle circonscrit au triangle ABC.

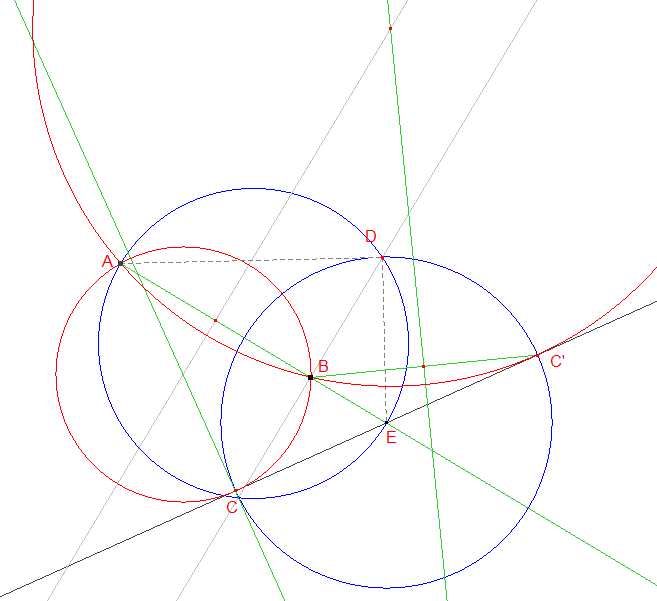
b) Analyse : Lorsque (AB) n'est pas parallèle à (d), supposons le problème résolu (cercle rouge ci-dessous). Notons E le point d'intersection des deux droites, et C le point de contact de (d) avec le cercle solution. On doit avoir EC² = EB × EA (» puissance d'un point par rapport à un cercle, cas de la tangente). Le problème revient à construire C et le cercle circonscrit au triangle ABC apparaîtra en tant que solution du problème initial.

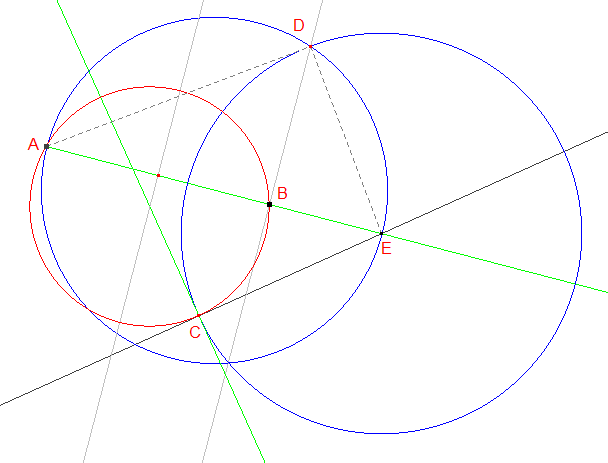
Synthèse : On trace le cercle de diamètre [AE]. La perpendiculaire à (AE) passant par B coupe ce cercle en deux points. Soit D l'un deux. Le cercle de centre E passant par D coupe (d) en C. ADE est rectangle en D. (DB) est la hauteur issue de D : on a ED² = EB.EA (» relations métriques dans le triangle rectangle) et ED = EC, donc EC² = EB.EA : c'est dire que (EC) est la tangente en C au cercle circonscrit au triangle ABC (» puissance d'un point par rapport à un cercle, cas de la tangente) qui est donc bien une solution du problème. Un seconde solution est obtenue en considérant C', symétrique de C par rapport à E, cercle circonscrit au triangle ABC'.