
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Un petit problème facile niveau CM2/6ème/5ème. On trouvera beaucoup plus difficile en chèvre de Monsieur Poincaré (niveau sup).
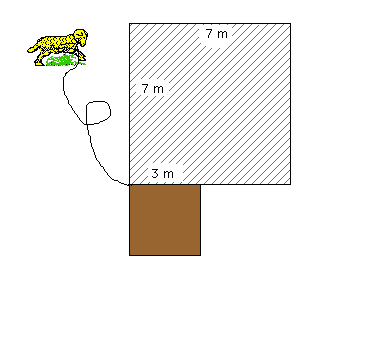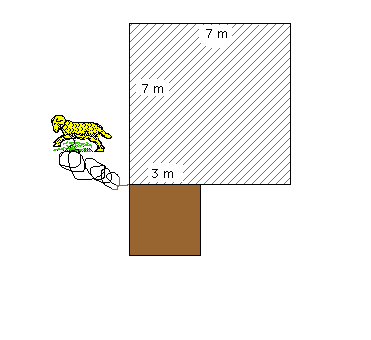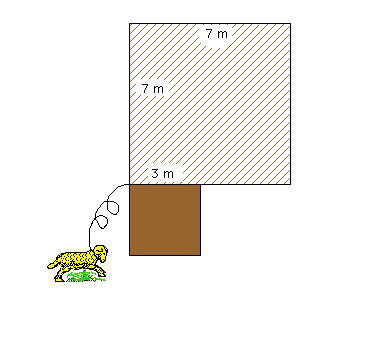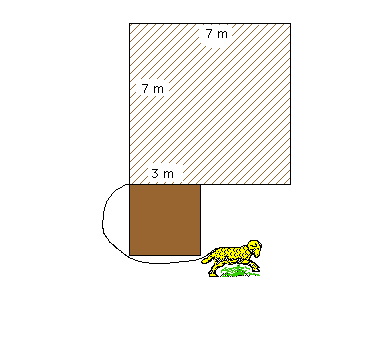
Une gentil petit mouton est tenu en laisse par une méchante corde de 9 m, elle-même fichée en terre par un piquet comme indiqué ci-dessus. La grange hachurée et le petit abri marron ne sont bien sûr pas accessibles.
• 1° - niveau CM2/6è/5è : à l'aide du compas, représente la surface où peut brouter le gentil petit mouton.
• 2° - niveau 6è/5è : calcule le périmètre de la surface que tu as trouvée.
• 3° - niveau 5è : calcule l'aire de cette surface.
• 4° - niveau 4è/3è : reprendre le problème 1 si le mouton est attaché au coin sud-ouest (bas-gauche) de l'abri marron.
➔ Depuis quelques années, les élèves de 6è n'ont plus droit à l'aire du cercle (du disque, plus précisément). Mais certains élèves la connaissent déjà depuis l'école primaire...
Si tu sèches après avoir bien cherché : ››››
| Solution : |

(1/4 × 4π) + (1/2 × 18π) + (1/4 × 12π) + (1/4 × 6π) + 3 × 3 + 7 + 2 = 14,5π + 18, soit 63,55 m à 0,01 près.
π × (22/4 + 92/2 + 62/4 + 32/4) = π (1 + 81/2 + 9 + 9/4) = 52,75π, soit 165,72 m2 à 0,01 près.
4° - Le mouton peut brouter dans les 3/4 d'un disque de rayon 9 m autour du piquet P (zone vert clair). Le secteur AED contient le point C qui est la limite sud-est de la grange hachurée. Il a pour rayon AD = 6 m car PA = 3 m. Il nous reste le petit secteur CFE : en appliquant le théorème de Pythagore au triangle rectangle de côtés 3 et 4, on obtient AC = 5, d'où CE = 6 - 5 = 1.
» triangle égyptien (niveau 4è/2nde)