
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
|
Un AirBus reliant Abidjan (Côte d'Ivoire) via Bamako (Mali) décolle de Paris rempli au trois quarts de sa capacité en passagers.
Six heures plus tard, il atterrit à Bamako où la moitié des passagers débarque.
128 nouveaux voyageurs montent à bord.
L'appareil décolle alors vers Abidjan avec 72 places vides.
Une heure 10 plus tard, la tour de contrôle d'Abidjan repère l'appareil.
Pourriez-vous préciser la capacité en passagers de cet appareil ?
Si vous séchez après avoir bien cherché : ››››
| Solution : |
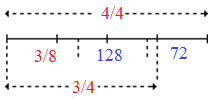

Si x désigne la capacité en passagers, l'énoncé conduit au petit schéma ci-dessus dont on déduit l'équation :
Résolution :
3x/8 + 128 + 72 = x ⇔ x - 3x/8 = 200 ⇔ 5x/8 = 200 ⇔ 5x = 1600 ⇔ x = 1600 ÷ 5 = 320
La capacité de cet avion est de 320 passagers.

Allergique aux équations ?
Au départ de Paris l'avion est plein aux 3/4, soit 6/8 (six huitièmes). A Bamako, la moitié débarque : il contient alors 3/8 (trois huitièmes) de sa capacité.
La capacité totale est 8/8 (huit huitièmes) et
8/8 - 3/8 = 5/8.
Donc 5/8 représentent au décollage vers
Abidjan 128 + 72 = 200 passagers.
Par conséquent 1/8 représente 200/5 = 40 passagers. La capacité totale (8/8), représente 8 fois plus, c'est à dire 320 passagers.
