
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
|

L'aire des trapèzes de base doit être maximale. Calculons cette aire : elle est fonction de x et de l'angle â comme indiqués sur la figure.
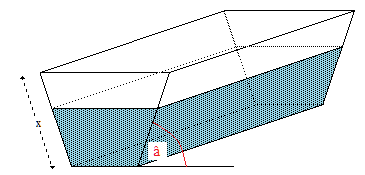
La hauteur sera h =
x![]() sin
sin![]() â;
â;
La petite base b mesurera 1,5 - 2x;
La grande base B sera 1,5 - 2x
+ 2x![]() cos
cos![]() â.
â.
L'aire A est donnée par la formule bien connue (B + b) × h/2 qui conduit après simplification à :
A = 1,5x![]() sin
sin![]() â
- 2x2sin
â
- 2x2sin![]() â
+ x2sin
â
+ x2sin![]() âcos
âcos![]() â
â
On applique la condition nécessaire d'extremum, à savoir :
∂A/∂x = ∂A/∂â = 0
Le calcul des dérivées partielles est simple. On devra trouver :
∂A/∂x
= sin![]() â(1,5 - 4x
+ 2x
â(1,5 - 4x
+ 2x![]() cos
cos![]() â) = 0
â) = 0
∂A/∂â
= x(1,5cos![]() â -
2x
â -
2x![]() cos
cos![]() â +
x
â +
x![]() cos
cos![]() 2â) = 0
2â) = 0
Les cas sin![]() â = 0 et
x = 0 étant
évidemment à rejeter, on tire de la première condition :
â = 0 et
x = 0 étant
évidemment à rejeter, on tire de la première condition :
x = 0,75/(2 - cos![]() â)
â)
et on reporte dans la seconde où l'on
remplacera cos![]() 2a par 2cos2a - 1. On trouvera sans difficulté la
réponse simplissime cos
2a par 2cos2a - 1. On trouvera sans difficulté la
réponse simplissime cos![]() â = 1/2, correspondant donc à un angle de 60°.
â = 1/2, correspondant donc à un angle de 60°.
D'où x = 0,5 : on constate donc qu'il faut plier la plaque au 1/3 et au 2/3.
➔ Partant d'un volume nul (â = 0), le pliage augmente le volume : notre extremum est plus que certainement un maximum...
Mais on peut vérifier cela en calculant les dérivées partielles d'ordre 2 au point trouvé :
∂2A/∂x2
= sin![]() â(2cos
â(2cos![]() â - 4) = -3√3/2
< 0
â - 4) = -3√3/2
< 0
∂2A/∂â2
= - x(1,5sin![]() â
+ 2x
â
+ 2x![]() sin
sin![]() â + 2x
â + 2x![]() sin
sin![]() 2â)
= -7√3/2
2â)
= -7√3/2
∂2A/∂x∂â
= cos![]() â(1,5 - 4x
+ 2x
â(1,5 - 4x
+ 2x![]() cos
cos![]() â) - 2xsin2â
= -3/4
â) - 2xsin2â
= -3/4
D =
∂2A/∂x2 ×
∂2A/∂x2
- (∂2A/∂x2)2
est donc strictement positif avec
∂2A/∂x2
> 0 : c'est un maximum.