
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

 |
|
Dans un disque de rayon R, comment découper une plaque quadrilatérale d'aire maximale ?
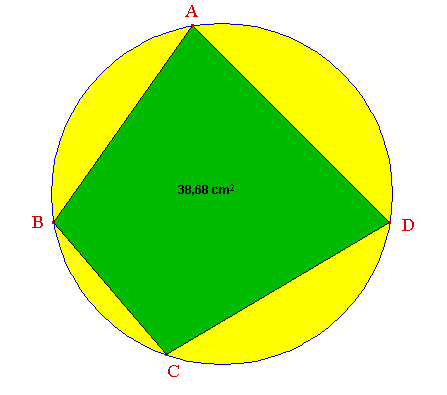
➔ Si votre navigateur le permet, voici la même figure générée par Cabri Géomètre dans sa version CabriJava pour Internet :

Indications :
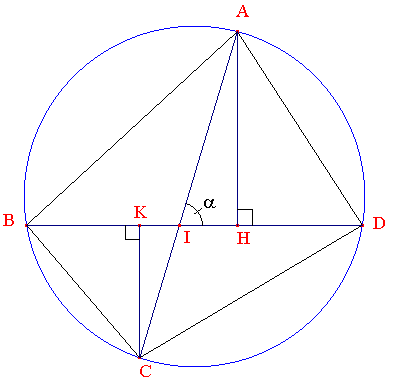
• Justifier par un dessin que toute plaque découpée dans l'intérieur du disque n'est pas solution.
• Soit ABCD un quadrilatère convexe inscrit dans le bord (c) de la plaque. Avec les notations de la figure ci-contre, montre que l'aire du quadrilatère ABCD est :
BD × (AH + CK)/2 (1)
• Exprime AH et CK au moyen de sinα et déduis de (1) que l'aire du quadrilatère ABCD est :
• Déduire de ce résultat que la solution est une plaque carrée inscrite dans le bord (c) et dont l'aire est 2R2.
➔ Sans passer par la trigonométrie, on peut déduire la solution à partir de la formule (1) : l'aire sera maximale si les longueurs BD et AH + CK sont maximales.
BD et AH + CK ne peuvent excéder le diamètre du cercle. AH + CK égalera un diamètre si et seulement si A et C sont diamétralement opposés. [BD] et [AC] sont alors des diamètres perpendiculaires du cercle : ABCD est un carré.